
【题目】某市一所高中为备战即将举行的全市羽毛球比赛,学校决定组织甲、乙两队进行羽毛球对抗赛实战训练.每队四名运动员,并统计了以往多次比赛成绩,按由高到低进行排序分别为第一名、第二名、第三名、第四名.比赛规则为甲、乙两队同名次的运动员进行对抗,每场对抗赛都互不影响,当甲、乙两队的四名队员都进行一次对抗赛后称为一个轮次.按以往多次比赛统计的结果,甲、乙两队同名次进行对抗时,甲队队员获胜的概率分别为![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)进行一个轮次对抗赛后一共有多少种对抗结果?
(2)计分规则为每次对抗赛获胜一方所在的队得1分,失败一方所在的队得0分,设进行一个轮次对抗赛后甲队所得分数为X,求X的分布列及数学期望.
科目:高中数学 来源: 题型:
【题目】某商家统计了去年![]() ,
,![]() 两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中
两种产品的月销售额(单位:万元),绘制了月销售额的雷达图,图中![]() 点表示
点表示![]() 产品2月份销售额约为20万元,
产品2月份销售额约为20万元,![]() 点表示
点表示![]() 产品9月份销售额约为25万元.
产品9月份销售额约为25万元.
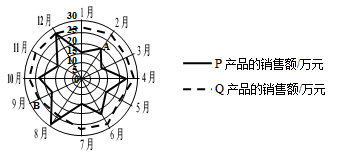
根据图中信息,下面统计结论错误的是( )
A.![]() 产品的销售额极差较大B.
产品的销售额极差较大B.![]() 产品销售额的中位数较大
产品销售额的中位数较大
C.![]() 产品的销售额平均值较大D.
产品的销售额平均值较大D.![]() 产品的销售额波动较小
产品的销售额波动较小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆M与直线![]() 相切,且与圆N:
相切,且与圆N:![]() 外切
外切
(1)求动圆圆心M的轨迹C的方程;
(2)点O为坐标原点,过曲线C外且不在y轴上的点P作曲线C的两条切线,切点分别记为A,B,当直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() 时,求证:直线
时,求证:直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某港口某天0时至24时的水深![]() (米)随时间
(米)随时间![]() (时)变化曲线近似满足如下函数模型
(时)变化曲线近似满足如下函数模型![]() (
(![]() ).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
).若该港口在该天0时至24时内,有且只有3个时刻水深为3米,则该港口该天水最深的时刻不可能为( )
A.16时B.17时C.18时D.19时
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位
平均增加5个单位
③线性回归方程![]() 必过
必过![]()
④设具有相关关系的两个变量![]() 的相关系数为
的相关系数为![]() ,那么
,那么![]() 越接近于0,
越接近于0,![]() 之间的线性相关程度越高;
之间的线性相关程度越高;
⑤在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,那么
的值,那么![]() 的值越大,判断两个变量间有关联的把握就越大。
的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com