
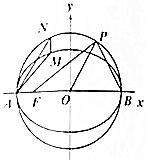
 已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.
已知椭圆C1:$\frac{{x}^{2}}{4}$+y2=1和圆C2:x2+y2=4,A,B,F分别为椭圆C1左顶点、右顶点和左焦点.分析 (1)由已知椭圆方程求出F的坐标,设出P的坐标,再由三角形面积求出P的坐标,可得△BOP为等边三角形,则答案可求;
(2)设直线AM的斜率为k,则直线AN的斜率为2k,又两直线都过点A(-1,0),可得直线AM的方程为y=kx+k,直线AN的方程为y=2kx+2k,分别联立直线方程与椭圆、圆的方程,求出M、N的横坐标得答案.
解答 (1)解:由椭圆C1:$\frac{{x}^{2}}{4}$+y2=1,得F(-$\sqrt{3}$,0),
设P(xP,yP)(xP>0,yP>0),
∵${S}_{△OPF}=\frac{1}{2}×\sqrt{3}{y}_{P}=\frac{3}{2}$,∴${y}_{P}=\sqrt{3}$,
则${{x}_{P}}^{2}=4-({y}_{P})^{2}=4-3=1$,∴xP=1.
则∠BOP=60°,∴△BOP为等边三角形,则∠OPB=60°;
(2)证明:设直线AM的斜率为k,则直线AN的斜率为2k,又两直线都过点A(-1,0),
∴直线AM的方程为y=kx+k,直线AN的方程为y=2kx+2k,
将y=kx+k代入椭圆方程$\frac{{x}^{2}}{4}$+y2=1,消元可得(1+4k2)x2+8k2x+4k2-4=0,
由${x}_{M}-1=\frac{-8{k}^{2}}{1+4{k}^{2}}$,得${x}_{M}=\frac{1-4{k}^{2}}{1+4{k}^{2}}$;
将y=2kx+2k代入x2+y2=4,消元可得(1+4k2)x2+8k2x+4k2-4=0,
由${x}_{N}-1=\frac{-8{k}^{2}}{1+4{k}^{2}}$,得${x}_{N}=\frac{1-4{k}^{2}}{1+4{k}^{2}}$.
∵xM=xN,∴直线MN⊥x轴.
点评 本题考查椭圆与圆的标准方程,考查直线与椭圆的位置关系,确定两点的横坐标是关键,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
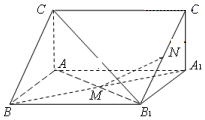 如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点
如图,直三棱柱ABC-A1B1C1中,M,N分别为A1B,B1C1的中点查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{2}}{3}$+1 | B. | 2$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{2}$+3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
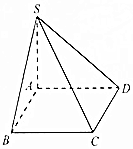 如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com