
已知正三棱柱ABC-A1B1C1的底面边长为2cm,高为4cm,过BC作一截面,截面与底面成![]() ,截面的面积是________.
,截面的面积是________.
|
思路 如下图所示,从确定截面的形状入手.
解答 不妨设过BC的截面与侧棱AA1(或延长线)相交于P点(如图所示),取BC的中点D.连结PD,AD,由对称性知PD⊥BC,AD⊥BC,则截面PBC与底面ABC所成二面角的平面角为∠PDA. 由题设知∠PDA= 因为AD= 所以PA=PDtan∠PDA= 从而P点在侧棱AA1上,故截面为△PBC. 因为PD=2AD=2 所以S△PBC= 评析 求截面的面积,首先要确定截面的形状.此题中如果PA>A1A,则截面是一个梯形. |


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
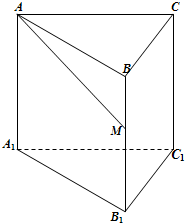 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
| AM |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
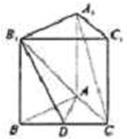 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com