已知数列{an}的前项和为Sn,点(an+2,Sn+1)在直线y=4x-5上,其中n∈N,令bn=an+1-2an,且a1=1.
(1)求证数列{bn}是等比数列;
(2)求数列{nbn}的前n项和Tn.
解:(1)因为点(a
n+2,S
n+1)在直线y=4x-5上;
∴S
n+1=4(a
n+2)-5=4a
n+3; ①
s
2=4a
1+3=a
1+a
2?a
2=4;
∴S
n=4a
n-1+3;②
∴①-②:a
n+1=4a
n-4a
n-1;
∴a
n+1-2a
n=2(a
n-2a
n-1);
数列{a
n-2a
n-1}是以2为首相,2为公比的等比数列;
即数列{b
n}是等比数列;
所以:b
n=a
n+1-2a
n=2
n+1;
(2)∵nb
n=n•2
n+1;
∴T
n=1×2
2+2×2
3+3×2
4+…+n•2
n+1;③
∴2T
n=1×2
3+2×2
4+…+(n-1)•2
n+1+n•2
n+2;④
③-④:-T
n=1×2
2+2
3+2
4+…+2
n+1-n•2
n+2=

-n•2
n+2=4+(1-n)•2
n+2;
∴
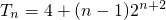
.
分析:(1)先根据已知条件得到S
n+1=4(a
n+2)-5=4a
n+3; 进而得到S
n=4a
n-1+3;另个等式相结合即可得到数列{a
n-2a
n-1}是以2为首相,2为公比的等比数列,即数列{b
n}是等比数列;
(2)先求出数列{nb
n}的通项公式,再利用错位相减法求数列{nb
n}的前n项和T
n.
点评:本题主要考查数列通项公式与前n项和之间的关系,以及错位相减法求和.

 -n•2n+2=4+(1-n)•2n+2;
-n•2n+2=4+(1-n)•2n+2;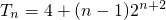 .
.
