
【题目】下列说法正确的是( )
A.若“![]() ”为真命题,则“
”为真命题,则“![]() ”为真命题
”为真命题
B.命题“![]() ”的否定是“
”的否定是“![]() ”
”
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
科目:高中数学 来源: 题型:
【题目】在直角坐标坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),曲线
为参数),曲线![]() :
: ![]() .以
.以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴,与直角坐标系
轴的非负半轴为极轴,与直角坐标系![]() 取相同的长度单位,建立极坐标系.
取相同的长度单位,建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的异于极点的交点为
的异于极点的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求
,求![]() .
.
【答案】(1) ![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() 的极坐标方程为
的极坐标方程为![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)先根据三角函数平方关系消参数得曲线![]() ,再根据
,再根据![]() 将曲线
将曲线![]() 的
的![]() 极坐标方程;(2)将
极坐标方程;(2)将![]() 代人曲线
代人曲线![]() 的极坐标方程,再根据
的极坐标方程,再根据![]() 求
求![]() .
.
试题解析:(1)曲线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
可化为普通方程![]() ,
,
由![]() ,可得曲线
,可得曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(2)射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径为
的极径为![]() ,
,
射线![]() (
(![]() )与曲线
)与曲线![]() 的交点
的交点![]() 的极径满足
的极径满足![]() ,解得
,解得![]() ,
,
所以![]() .
.
【题型】解答题
【结束】
23
【题目】设函数![]() .
.
(1)设![]() 的解集为
的解集为![]() ,求集合
,求集合![]() ;
;
(2)已知![]() 为(1)中集合
为(1)中集合![]() 中的最大整数,且
中的最大整数,且![]() (其中
(其中![]() ,
,![]() ,
,![]() 为正实数),求证:
为正实数),求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设抛物线C1:![]() 的准线1与x轴交于椭圆C2:
的准线1与x轴交于椭圆C2:![]() 的右焦点F2,F1为C2的左焦点.椭圆的离心率为
的右焦点F2,F1为C2的左焦点.椭圆的离心率为![]() ,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.

(1)当![]() 取最小值时,求C1和C2的方程;
取最小值时,求C1和C2的方程;
(2)若△PF1F2的边长恰好是三个连续的自然数,当△MPQ面积取最大值时,求面积最大值以及此时直线MP的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数且
为参数且![]() ,
,![]() ,
,![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程及
的普通方程及![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 分别交于点
分别交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富学生课外生活,某市组织了高中生钢笔书法比赛,比赛分两个阶段进行:第一阶段由评委给出所有参赛作品评分,并确定优胜者;第二阶段为附加赛,参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析,这些分数![]() 都在
都在![]() 内,在以组距为5画分数的频率分布直方图(设“
内,在以组距为5画分数的频率分布直方图(设“![]() ”)时,发现
”)时,发现![]() 满足
满足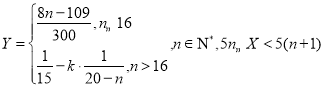 .
.
(1)试确定![]() 的所有取值,并求
的所有取值,并求![]() ;
;
(2)组委会确定:在第一阶段比赛中低于85分的参赛者无缘获奖也不能参加附加赛;分数在![]() 的参赛者评为一等奖;分数在
的参赛者评为一等奖;分数在![]() 的同学评为二等奖,但通过附加赛有
的同学评为二等奖,但通过附加赛有![]() 的概率提升为一等奖;分数在
的概率提升为一等奖;分数在![]() 的同学评为三等奖,但通过附加赛有
的同学评为三等奖,但通过附加赛有![]() 的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生
的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级).已知学生![]() 和
和![]() 均参加了本次比赛,且学生
均参加了本次比赛,且学生![]() 在第一阶段评为二等奖.
在第一阶段评为二等奖.
(![]() )求学生
)求学生![]() 最终获奖等级不低于学生
最终获奖等级不低于学生![]() 的最终获奖等级的概率;
的最终获奖等级的概率;
(![]() )已知学生
)已知学生![]() 和
和![]() 都获奖,记
都获奖,记![]() 两位同学最终获得一等奖的人数为
两位同学最终获得一等奖的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在中国决胜全面建成小康社会的关键之年,如何更好地保障和改善民生,如何切实增强政策“获得感”,成为2019年全国两会的重要关切.某地区为改善民生调研了甲、乙、丙、丁、戊5个民生项目,得到如下信息:
①若该地区引进甲项目,就必须引进与之配套的乙项目;
②丁、戊两个项目与民生密切相关,这两个项目至少要引进一个;
③乙、丙两个项目之间有冲突,两个项目只能引进一个;
④丙、丁两个项目关联度较高,要么同时引进,要么都不引进;
⑤若引进项目戊,甲、丁两个项目也必须引进.
则该地区应引进的项目为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC-A1B1C1中,侧面BCC1B1是菱形,AC=BC=2,∠CBB1=![]() ,点A在平面BCC1B1上的投影为棱BB1的中点E.
,点A在平面BCC1B1上的投影为棱BB1的中点E.
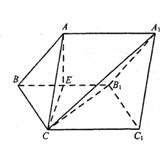
(1)求证:四边形ACC1A1为矩形;
(2)求二面角E-B1C-A1的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: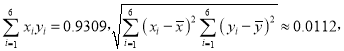
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com