
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)讨论![]() 在
在![]() 上的零点个数.
上的零点个数.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上单调递减,当
上单调递减,当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)当
上单调递减;(2)当![]() 时,
时,![]() 在
在![]() 上没有零点,当
上没有零点,当![]() 时,
时,![]() 在
在![]() 上只有一个零点,当
上只有一个零点,当![]() 时,
时,![]() 在
在![]() 上有两个零点.
上有两个零点.
【解析】
(1)利用函数![]() 的导函数,分类讨论参数
的导函数,分类讨论参数![]() ,得出
,得出![]() 的单调性;
的单调性;
(2)转化问题,原函数有零点即函数![]() 有解,求导得出
有解,求导得出![]() 的单调性和极值,分类讨论得出
的单调性和极值,分类讨论得出![]() 在
在![]() 上的零点个数.
上的零点个数.
解:(1)∵![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() 恒成立,
恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,
令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() .
.
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
综上所述,当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;
上单调递减;
(2)令![]() ,得
,得![]() ,
,
设![]() ,则
,则![]() .
.
令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,则
上单调递增,则![]() .
.
当![]() 时,
时,![]() 在
在![]() 上无解,所以
上无解,所以![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 时,
时,![]() 在
在![]() 上有且仅一个解,所以
上有且仅一个解,所以![]() 在
在![]() 上有一个零点;
上有一个零点;
当![]() 时,
时,![]() 在
在![]() 上有两个解,所以
上有两个解,所以![]() 在
在![]() 上有两个零点.
上有两个零点.
综上,当![]() 时,
时,![]() 在
在![]() 上没有零点;
上没有零点;
当![]() 时,
时,![]() 在
在![]() 上只有一个零点;
上只有一个零点;
当![]() 时,
时,![]() 在
在![]() 上有两个零点.
上有两个零点.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中数学 来源: 题型:
【题目】2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
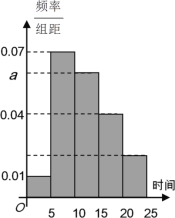
(1)求![]() 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
(2)现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ;
;
(Ⅰ)若函数![]() 在[1,2]上是减函数,求实数
在[1,2]上是减函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)令![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() (
(![]() 是自然对数的底数)时,函数
是自然对数的底数)时,函数![]() 的最小值是
的最小值是![]() .若存在,求出
.若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】詹姆斯·哈登(James Harden)是美国NBA当红球星,自2012年10月加盟休斯顿火箭队以来,逐渐成长为球队的领袖.2017-18赛季哈登当选常规赛MVP(最有价值球员).
年份 | 2012-13 | 2013-14 | 2014-15 | 2015-16 | 2016-17 | 2017-18 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
常规赛场均得分y | 25.9 | 25.4 | 27.4 | 29.0 | 29.1 | 30.4 |
(Ⅰ)根据表中数据,求y关于t的线性回归方程![]() (
(![]() ,
,![]()
![]() *);
*);
(Ⅱ)根据线性回归方程预测哈登在2019-20赛季常规赛场均得分.
(附)对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:![]() ,
,![]()
(参考数据![]() ,计算结果保留小数点后一位)
,计算结果保留小数点后一位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量![]() 万件(生产量与销售量相等)与推广促销费
万件(生产量与销售量相等)与推广促销费![]() 万元之间的函数关系为
万元之间的函数关系为![]() (其中推广促销费不能超过5千元).已知加工此农产品还要投入成本
(其中推广促销费不能超过5千元).已知加工此农产品还要投入成本![]() 万元(不包括推广促销费用),若加工后的每件成品的销售价格定为
万元(不包括推广促销费用),若加工后的每件成品的销售价格定为![]() 元/件.
元/件.
(1)试将该批产品的利润![]() 万元表示为推广促销费
万元表示为推广促销费![]() 万元的函数;(利润=销售额-成本-推广促销费)
万元的函数;(利润=销售额-成本-推广促销费)
(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以 A 为圆心, 以![]() 为半径的圆外有一点 B , 已知
为半径的圆外有一点 B , 已知 ![]() =2sinθ.设过点B且与⊙A 外切于点T的圆的圆心为 M.
=2sinθ.设过点B且与⊙A 外切于点T的圆的圆心为 M.
(1)当 θ取某个值时, 说明点 M 的轨迹P 是什么曲线;
(2)点M 是轨迹 P上的动点, 点N 是 ⊙A上的动点, 把![]() 的最小值记为
的最小值记为![]() (不要求证明), 求
(不要求证明), 求![]() 的取值范围;
的取值范围;
(3)若将题设条件中的θ的范围改为![]() ,点 B 的位置改为⊙A内 , 其它条件不变,点 M的轨迹记为 P .试提出一个和(2)具有相同结构的有意义的问题(不要求解答).
,点 B 的位置改为⊙A内 , 其它条件不变,点 M的轨迹记为 P .试提出一个和(2)具有相同结构的有意义的问题(不要求解答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com