练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    关于函数f(x)＝sin2x－()|x|＋，有下面四个结论，其中正确结论的个数为①f(x)是奇函数　②当x＞2003时，f(x)＞恒成立　③f(x)的最大值是　④f(x)的最小值是－

    [　　]

    A．1

    B．2

    C．3

    D．4

    答案：A
    解析：

    　　显然f(x)为偶函数，结论①错．对于结论②，当x＝1000π时，x＞2003，sin21000π＝0，∴f(1000π)＝－()1000π＜，因此结论②错．

    　　又f(x)＝－()|x|＋＝1－cos2x－()|x|，－1≤cos2x≤1，

    　　∴－≤1－cos2x≤．

    　　故1－cos2x－()|x|＜，即结论③错．

    　　而cos2x，()|x|在x＝0时同时取得最大值，

    　　所以f(x)＝1－cos2x－()|x|在x＝0时可取得最小值－，

    　　即结论④是正确的．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：吉林省实验中学2012届高三第六次模拟考试数学理科试题 题型：022

    已知定义在[1，＋∞)上的函数f(x)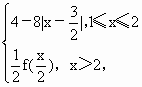＝．给出下列结论：

    ①函数f(x)的值域为[0，4]；

    ②关于x的方程f(x)＝()n(n∈N*)有2n＋4个不相等的实数根；

    ③当x∈[2n－1，2n](n∈N*)时，函数f(x)的图象与x轴围成的图形面积为S，则S＝2；

    ④存在x0∈[1，8]，使得不等式x0f(x0)＞6成立，

    其中你认为正确的所有结论的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：2013年普通高等学校招生全国统一考试天津卷理数 题型：044

    已知函数f(x)＝x2lnx．

    (Ⅰ)求函数f(x)的单调区间；

    (Ⅱ)证明：对任意的t＞0，存在唯一的s，使t＝f(s)．

    (Ⅲ)设(Ⅱ)中所确定的s关于t的函数为s＝g(t)，证明：当t＞e2时，有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知关于x的函数f(x)＝＋bx2＋cx＋bc,其导函数为f+(x).令g(x)＝∣f (x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.

       (Ⅰ)如果函数f(x)在x＝1处有极值-，试确定b、c的值：

      （Ⅱ）若∣b∣>1,证明对任意的c,都有M>2: w.w.w.k.s.5.u.c.o.m    

       (Ⅲ)若M≧K对任意的b、c恒成立，试求k的最大值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝ax3＋x2在x＝－1处取得极值，记g(x)＝，程序框图如图所示，若输出的结果S>，则判断框中可以填入的关于n的判断条件是                                   (　　)

    A．n≤2 011?                       B．n≤2 012?

    C．n>2 011?                        D．n>2 012?

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年江西赣州四所重点中学高三上学期期末联考理数学试卷（解析版） 题型：选择题

    已知函数f(x)＝ax3＋x2在x＝－1处取得极大值，记g(x)＝。程序框图如图所示，若输出的结果S＝，则判断框中可以填入的关于n的判断条件是（    ）

    A．n≤2013   B．n≤2014        C．n＞2013     D．n＞2014

     

    查看答案和解析>>

    同步练习册答案