
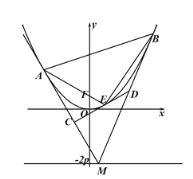
【题目】如图,设抛物线方程为![]() (p>0),M为直线
(p>0),M为直线![]() 上任意一点,过M引抛物线的切线,切点分别为A,B.
上任意一点,过M引抛物线的切线,切点分别为A,B.
(1)求直线AB与![]() 轴的交点坐标;
轴的交点坐标;
(2)若E为抛物线弧AB上的动点,抛物线在E点处的切线与三角形MAB的边MA,MB分别交于点![]() ,
,![]() ,记
,记![]() ,问
,问![]() 是否为定值?若是求出该定值;若不是请说明理由.
是否为定值?若是求出该定值;若不是请说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,底面是边长为4的正三角形,
中,底面是边长为4的正三角形,![]() ,
,![]() 底面
底面![]() ,点
,点![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
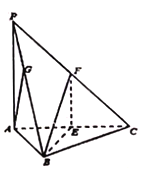
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查一款手机的使用时间,研究人员对该款手机进行了相应的测试,将得到的数据统计如下图所示:
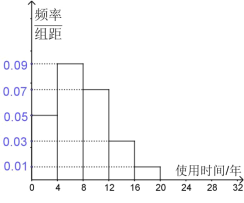
并对不同年龄层的市民对这款手机的购买意愿作出调查,得到的数据如下表所示:
愿意购买该款手机 | 不愿意购买该款手机 | 总计 | |
40岁以下 | 600 | ||
40岁以上 | 800 | 1000 | |
总计 | 1200 |
(1)根据图中的数据,试估计该款手机的平均使用时间;
(2)请将表格中的数据补充完整,并根据表中数据,判断是否有99.9%的把握认为“愿意购买该款手机”与“市民的年龄”有关.
参考公式: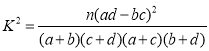 ,其中
,其中![]() .
.
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线
,圆心为坐标原点的单位圆O在C的内部,且与C有且仅有两个公共点,直线![]() 与C只有一个公共点.
与C只有一个公共点.
(1)求C的标准方程;
(2)设不垂直于坐标轴的动直线l过椭圆C的左焦点F,直线l与C交于A,B两点,且弦AB的中垂线交x轴于点P,试求![]() 的面积的最大值.
的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式.孪生素数猜想是希尔伯特在二十世纪初提出的23个数学问题之一.可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,称素数对
是素数,称素数对![]() 为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() ,以坐标原点
,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() .
.
(Ⅰ)求曲线![]() 被直线
被直线![]() 截得的弦长;
截得的弦长;
(Ⅱ)与直线![]() 垂直的直线
垂直的直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,求点
,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
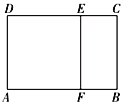
【题目】如图,四边形![]() 是矩形,
是矩形,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的一点,且
上的一点,且![]() ,
,![]() ,将矩形
,将矩形![]() 卷成以
卷成以![]() ,
,![]() 为母线的圆柱的半个侧面,且
为母线的圆柱的半个侧面,且![]() ,
,![]() 分别为圆柱的上、下底面的直径.
分别为圆柱的上、下底面的直径.
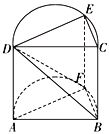
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com