Question

11．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（b＞a＞0）的正半轴焦点为F，负半轴焦点为F′，AA′为长轴，点Q为椭圆上任意一点，则分别以|QF|，|QF′|，|AA′|为直径的圆之间的位置关系说法正确的是（　　）

• A． 以|QF|为直径的圆与以|AA′|为直径的圆内切
• B． 以|QF′|为直径的圆与以|AA′|为直径的圆相交
• C． 以|QF|为直径的圆与以|AA′|为直径的圆相交
• D． 以|QF|为直径的圆与以|QF′|为直径的圆相切

Answer 1

分析 由椭圆的定义可得，|QF+|QF′|=2b，|AA′|=2b，由两圆的位置关系和三角形的中位线定理，即可判断A正确，B，C，D错误．

解答 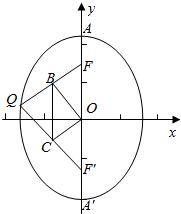解：由椭圆的定义可得，|QF+|QF′|=2b，|AA′|=2b，
对于A，以|QF|为直径的圆与以|AA′|为直径的圆心距为
|OB|=$\frac{1}{2}$|QF′|=b-$\frac{1}{2}$|QF|，即为两圆内切，故正确；
对于B，以|QF′|为直径的圆与以|AA′|为直径的圆心距为
|OC|=$\frac{1}{2}$|QF|=b-$\frac{1}{2}$|QF'|，即为两圆内切，故不正确；
对于C，由A可得两圆内切，故不正确；
对于D，以|QF|为直径的圆与以|QF'|为直径的圆心距为
|BC|=$\frac{1}{2}$|FF'|=c，而两圆的半径之和为b，两圆相交，故不正确．
故选：A．

点评 本题考查椭圆的定义，考查两圆的位置关系的判断，考查推理能力，属于中档题．