Question

【题目】在直角坐标系xOy中，以O为原点，Ox轴为极轴，单位长度不变，建立极坐标系，直线l的极坐标方程为：ρsin（θ+ ）= ，曲线C的参数方程为：
（1）写出直线l和曲线C的普通方程；
（2）若直线l和曲线C相交于A，B两点，定点P（﹣1，2），求线段|AB|和|PA||PB|的值．

Answer 1

【答案】
（1）解：直线l的极坐标方程为：ρsin（θ+ ）= ，

展开可得： ρ（sinθ+cosθ）= ，可得直角坐标方程：x+y﹣1=0．

曲线C的参数方程为： ，x2=4（1+sin2t）=y，x∈

（2）解：直线l的参数方程为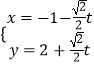： ，代入曲线C的方程可得： t﹣2=0，

∴t1+t2=﹣ ，t1t2=﹣2．

∴|AB|=|t1﹣t2|= = = ，

|PA||PB|=|t1t2|=2

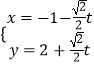【解析】（1）直线l的极坐标方程为：ρsin（θ+ ）= ，展开可得： ρ（sinθ+cosθ）= ，利用互化公式可得直角坐标方程．曲线C的参数方程为： ，可得x2=4（1+sin2t）=y，x∈ ．（2）直线l的参数方程为： ，代入曲线C的方程可得： t﹣2=0，可得|AB|=|t1﹣t2|= ，
|PA||PB|=|t1t2|．