练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    某公司为了了解职工的年龄分布，在甲乙两部门各随机抽取10名职工，统计他们的年龄，绘成茎叶图如右图所示：
    （Ⅰ）求甲部门职工年龄的众数与乙部门职工年龄的中位数.
    （Ⅱ）请判断哪个部门的职工年龄更年轻化，并说明你的理由.
    （Ⅰ）众数是32，中位数是26 {（24+28）/2}.
    （Ⅱ）甲部门职工年龄更年轻.
    (I)众数是出现频率最高的数.中位数是从小到大或从大到小排列位居中间的那个数，当数的个数是偶数时，取中间两个数的平均值.
    （II）分别算出甲部门职工和乙部门职工平均年龄，然后比较大小再确定哪个部门职工年龄更年轻.
    （Ⅰ）从图中可知，甲部门职工年龄的众数是32，乙部门职工年龄的中位数是26 {（24+28）/2}.
    （Ⅱ）甲部门职工年龄更年轻些，从茎叶图中的数据可算出，甲部门的平均年龄为27.1，乙部门平均年龄为27.5，故甲部门职工年龄更年轻
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （14分）某中学号召学生在今年春节期间至少参加一次社会公益活动（以下简称活动）。该校合唱团共有100名学生，他们参加活动的次数统计如图所示。

    ⑴求合唱团学生参加活动的人均次数；
    ⑵从合唱团中任选两名学生，求他们参加活动次数恰好相等的概率；
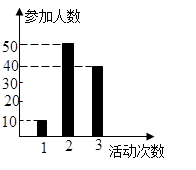
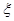    ⑶从合唱团中任选两名学生，用表示这两人参加活动次数之差的绝对值，求随机变量
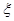    的分布列及数学期望。

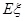    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设有两组数据x1，x2，…，xn与y1，y2，…，yn，它们的平均数分别是和，则新的一组数据2x1－3y1＋1,2x2－3y2＋1，…，2xn－3yn＋1的平均数是(　　)
    A．2－3　B．2－3＋1
    C．4－9D．4－9＋1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

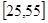    某同学在“两会”期间进行社会实践活动，对岁的人群随机抽取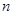人进行了一次居民对当前投资生活方式——“房地产投资”的调查，得到如下统计表和各年龄段人数频率分布直方图；
    组数
    		分组
    		房地产投资的人数
    		占本组的频率
    第一组
    		[25,30）
    		120
    		0.6
    第二组
    		[30,35）
    		195
    		p
    第三组
    		[35,40）
    		100
    		0.5
    第四组
    		[40,45）
    		a
    		0.4
    第五组
    		[45,50）
    		30
    		0.3
    第六组
    		[50,55]
    		15
    		0.3

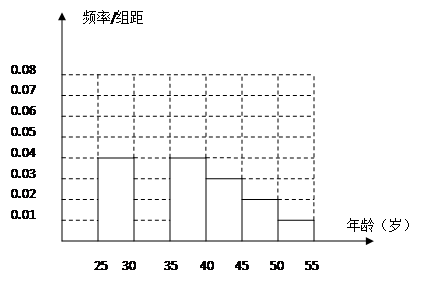
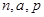    （1）补全频率分布直方图，并求出的值；
    （2）根据频率分布直方图，估计：“房地产投资”人群的平均年龄.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    在如图所示的茎叶图中，甲、乙两组数据的
    中位数分别是__________、___________.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

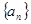    为了研究某高校大学新生学生的视力情况，随机地抽查了该校100名进校学生的视力情况，得到频率分布直方图,如图.已知前4组的频数从左到右依次是等比数列的前四项，后6组的频数从左到右依次是等差数列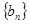的前六项．(Ⅰ)求等比数列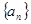的通项公式;
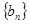    （Ⅱ）求等差数列的通项公式；(Ⅲ)若规定视力低于5.0的学生属于近视学生,试估计该校新生的近视率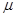的大小.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了解学生身高情况，某校以10%的比例对全校700名学生按性别进行分层抽样调查，测得身高情况的统计图如下：

    (1)估计该校男生的人数；
    (2)估计该校学生身高在170～185 cm之间的概率；
    (3)从样本中身高在180～190 cm之间的男生中任选2人，求至少有1人身高在185～190 cm之间的概率.

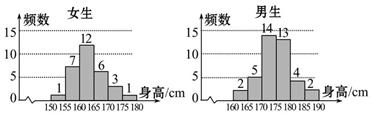
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

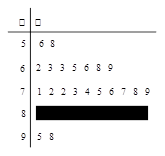
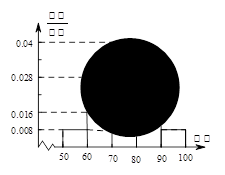
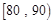    某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题．

    ⑴求全班人数及分数在之间的频数；
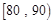    ⑵估计该班的平均分数，并计算频率分布直方图中间的矩形的高；
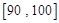    ⑶若要从分数在之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在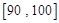之间的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

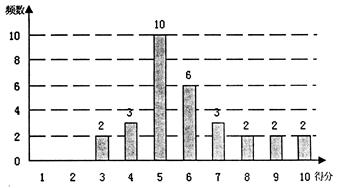
    某项测试成绩满分为10分，现随机抽取30名学生参加测试，得分如图所示，假设得分值的中位数为me，平均值为，众数为mo，则
    A．me＝mo＝
    B．me＝mo<
    C．me<m0<
    D．mo<me<

    查看答案和解析>>

    同步练习册答案