
【题目】解关于x的不等式:x2-(a+![]() )x+1≤0 (a∈R,且a≠0)
)x+1≤0 (a∈R,且a≠0)
【答案】当-1<a<0或a>1时,不等式的解集为[![]() ,a]; 当a<-1或0<a<1时,不等式的解集为[a,
,a]; 当a<-1或0<a<1时,不等式的解集为[a,![]() ]; 当a=-1时,不等式的解集为{-1}; 当a=1时,不等式的解集为{1};
]; 当a=-1时,不等式的解集为{-1}; 当a=1时,不等式的解集为{1};
【解析】
将不等式因式分解,得到两个零点。根据两个零点的大小,分类讨论a的取值情况,进而写出不等式的解集。
不等式可化为:(x-a)(x-![]() )≤0.
)≤0.
令(x-a)(x-![]() )=0,可得:x=a或x=
)=0,可得:x=a或x=![]() .
.
①当a>![]() ,即-1<a<0或a>1时,不等式的解集为[
,即-1<a<0或a>1时,不等式的解集为[![]() ,a];
,a];
②当a<![]() ,即a<-1或0<a<1时,不等式的解集为[a,
,即a<-1或0<a<1时,不等式的解集为[a,![]() ];
];
③当a=![]() ,即a=-1或a=1时,
,即a=-1或a=1时,
(i)若a=-1,则不等式的解集为{-1};
(ii)若a=1,则不等式的解集为{1}.
综上,当-1<a<0或a>1时,不等式的解集为[![]() ,a];
,a];
当a<-1或0<a<1时,不等式的解集为[a,![]() ];
];
当a=-1时,不等式的解集为{-1};
当a=1时,不等式的解集为{1};


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的半焦距为
的半焦距为![]() ,圆
,圆![]() 与椭圆
与椭圆![]() 有且仅有两个公共点,直线
有且仅有两个公共点,直线![]() 与椭圆
与椭圆![]() 只有一个公共点.
只有一个公共点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知动直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点,试问:
两点,试问:![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出该定值和点
为定值?若存在,求出该定值和点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别是a,b,c,若sin A+cos A=1-sin![]() .
.
(1)求sin A的值;
(2)若c2-a2=2b,且sin B=3cos C,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点为了了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图:

根据该折线图,下列结论正确的是( )
A.各年1月至8月月接待游客量逐月增加
B.各年8月至12月月接待游客量逐月递减
C.各年的月接待游客量最低峰期在12月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点,点M为BB1的中点.
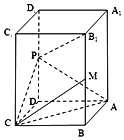
(1)求证:PB1⊥平面PAC;
(2)求直线CM与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,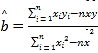 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com