
【题目】高中流行这样一句话“文科就怕数学不好,理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据,试问:在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗?
总成绩好 | 总成绩不好 | 总计 | |
数学成绩好 | 20 | 10 | 30 |
数学成绩不好 | 5 | 15 | 20 |
总计 | 25 | 25 | 50 |
(P(K2≥3.841)≈0.05,P(K2≥6.635)≈0.01)
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
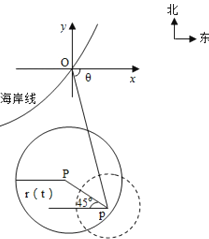
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市O(如图)的东偏南![]() 方向
方向![]() 的海面P处,且
的海面P处,且![]() ,并以
,并以![]() 的速度向西偏北
的速度向西偏北![]() 方向移动,台风侵袭的范围为圆形区域,当前半径为
方向移动,台风侵袭的范围为圆形区域,当前半径为![]() ,并以
,并以![]() 的速度不断增大,问几小时后该城市开始受到台风的侵袭?
的速度不断增大,问几小时后该城市开始受到台风的侵袭?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年出现各种食品问题,食品添加剂会引起血脂增高、血压增高、血糖增高等疾病.为了解三高疾病是否与性别有关,医院随机对入院的60人进行了问卷调查,得到了如下的列联表:
患三高疾病 | 不患三高疾病 | 合计 | |
男 | 6 | 30 | |
女 | |||
合计 | 36 |
下面的临界值表供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ![]() ,其中
,其中 ![]() )
)
(1)请将如图的列联表补充完整;若用分层抽样的方法在患三高疾病的人群中抽 ![]() 人,其中女性抽多少人?
人,其中女性抽多少人?
(2)为了研究三高疾病是否与性别有关,请计算出统计量 ![]() ,并说明你有多大的把握认为三高疾病与性别有关?
,并说明你有多大的把握认为三高疾病与性别有关?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+2)=f(x﹣2),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)有3个不同的实数根,则a的取值范围是( )
A.(1,2)
B.(2,+∞)
C.(1, ![]() )
)
D.( ![]() ,2)
,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某市学生百米运动成绩,从该市学生中按照男女生比例随机抽取50名学生进行百米测试,测试成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15),…,第五组[17,18],如图是按上述分组方法得到的频率分布直方图.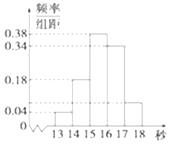
(1)设m,n表示样本中两个学生的百米测试成绩,已知m,n∈[13,14)∪[17,18],求事件“|m-n|>2”的概率;
(2)根据有关规定,成绩小于16秒为达标.
如果男女生使用相同的达标标准,则男女生达标情况如附表:
根据上表数据,能否在犯错误的概率不超过0.01的前提下认为“体育达标与性别有关”?若有,你能否提出一个更好的解决方法来?
附: 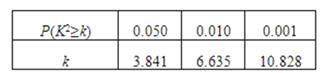
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=![]() ,动点D在线段AB上.
,动点D在线段AB上.

(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+1(a,b为实数),x∈R, ![]()
(1)若f(﹣1)=0,且函数f(x)的值域为[0,+∞),求F(x)的表达式;
(2)在(1)的条件下,当x∈[﹣2,2]时,g(x)=f(x)﹣kx是单调函数,求实数k的取值范围;
(3)设mn<0,m+n>0,a>0且f(x)为偶函数,判断F(m)+F(n)能否大于零.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知点P在☉O外,PC是☉O的切线,切点为C,直线PO与☉O相交于点A,B. 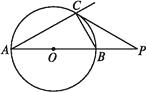
(1)试探索∠BCP与∠P的数量关系;
(2)若∠A=30°,则PB与PA有什么关系?
(3)∠A可能等于45°吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com