Question

已知集合A={x|x²-5x+6=0}，B={x|mx+1=0}，且A∪B=A，则实数m组成的集合    ．

Answer 1

【答案】分析：集合A={2，3}，由A∪B=A，可得 B⊆A，B中这多有一个元素．分B=∅、B={2 }、B={3 }，分别求得实数m的值，即可得到所求．
解答：解：集合A={x|x²-5x+6=0}={2，3}，B={x|mx+1=0}，且A∪B=A，∴B⊆A，B中这多有一个元素．
当 B=∅时，m=0．
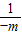
当 B={2 }时，有 =2，解得 m=-．
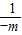
当 B={3} 时，有 =3，解得 m=-．
综上可得，实数m组成的集合为 {}，
故答案为{  }．
点评：本题主要考查集合关系中参数的取值范围问题，两个集合的交集、并集的定义，属于基础题．