
°æƒø°ø‘⁄¥´»æ≤°—ß÷–£¨Õ®≥£∞—¥”÷¬≤°¥Ãº§ŒÔ«÷»Îª˙êڒfl∂‘ª˙ÃÂ∑¢…˙◊˜”√∆£¨µΩª˙ÃÂ≥ˆœ÷∑¥”¶ªÚø™ º≥ œ÷∏√º≤≤°∂‘”¶µƒœ‡πÿ÷¢◊¥ ±÷𵃒‚“ªΩ◊∂Œ≥∆Œ™«±∑¸∆⁄.“ª—–æøÕ≈∂”Õ≥º∆¡Àƒ≥µÿ«¯200√˚ªº’flµƒœ‡πÿ–≈œ¢£¨µ√µΩ»Áœ¬±Ì∏Ò£∫
«±∑¸∆⁄£®µ•Œª£∫ÃÏ£© |
|
|
|
|
|
|
|
»À ˝ | 17 | 41 | 62 | 50 | 26 | 3 | 1 |
£®1£©«Û’‚200√˚ªº’flµƒ«±∑¸∆⁄µƒ—˘±æ∆Ωæ˘ ˝![]() £®Õ¨“ª◊È÷–µƒ ˝æ›”√∏√◊È«¯º‰µƒ÷–µ„÷µ◊˜¥˙±Ì£©£ª
£®Õ¨“ª◊È÷–µƒ ˝æ›”√∏√◊È«¯º‰µƒ÷–µ„÷µ◊˜¥˙±Ì£©£ª
£®2£©∏√¥´»æ≤°µƒ«±∑¸∆⁄ ‹÷Ó∂‡“ÚÀÿµƒ”∞œÏ£¨Œ™—–æø«±∑¸∆⁄”Ϊº’flƒÍ¡‰µƒπÿœµ£¨“‘«±∑¸∆⁄ «∑Ò≥¨π˝6ÃÏŒ™±Í◊ºΩ¯––∑÷≤„≥È—˘£¨¥”…œ ˆ200√˚ªº’fl÷–≥È»°40»Àµ√µΩ»Áœ¬¡–¡™±Ì.«ÎΩ´¡–¡™±Ì≤π≥‰ÕÍ’˚£¨≤¢∏˘æ›¡–¡™±Ì≈–∂œ «∑Ò”–95%µƒ∞—Œ’»œŒ™«±∑¸∆⁄”Ϊº’flƒÍ¡‰”–πÿ£ª
«±∑¸∆⁄ | «±∑¸∆⁄ | ◊‹º∆ | |
50ÀÍ“‘…œ£®∫¨50ÀÍ£© | 20 | ||
50ÀÍ“‘œ¬ | 9 | ||
◊‹º∆ | 40 |
£®3£©“‘’‚200√˚ªº’flµƒ«±∑¸∆⁄≥¨π˝6Ãϵƒ∆µ¬ £¨¥˙ÃÊ∏√µÿ«¯1√˚ªº’fl«±∑¸∆⁄≥¨π˝6ÃÏ∑¢…˙µƒ∏≈¬ £¨√ø√˚ªº’flµƒ«±∑¸∆⁄ «∑Ò≥¨π˝6ÃÏœ‡ª•∂¿¡¢.Œ™¡À…Ó»Î≥xæø£¨∏√—–æøÕ≈∂”‘⁄∏√µÿ«¯Àʪ˙µ˜≤È¡À10√˚ªº’fl£¨∆‰÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝◊Ó”–ø…ƒ‹£®º¥∏≈¬ ◊Ó¥Û£© «∂‡…Ÿ£ø
∏Ω£∫
| 0.05 | 0.025 | 0.010 |
| 3.841 | 5.024 | 6.635 |
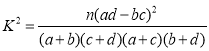 £¨∆‰÷–
£¨∆‰÷–![]()
°æ¥∞∏°ø£®1£©![]() £®ÃÏ£©£®2£©Ãӱ̺˚Ω‚Œˆ£ª√ª”–
£®ÃÏ£©£®2£©Ãӱ̺˚Ω‚Œˆ£ª√ª”–![]() µƒ∞—Œ’»œŒ™«±∑¸∆⁄”Ϊº’flƒÍ¡‰”–πÿ£®3£©◊Ó”–ø…ƒ‹ «4»À
µƒ∞—Œ’»œŒ™«±∑¸∆⁄”Ϊº’flƒÍ¡‰”–πÿ£®3£©◊Ó”–ø…ƒ‹ «4»À
°æΩ‚Œˆ°ø
£®1£©¿˚”√∆Ωæ˘÷µµƒ∂®“«ÛΩ‚º¥ø…£ª
£®2£©∏˘æ›Ã‚ƒøÀ˘∏¯µƒ ˝æ›ÃÓ–¥2°¡2¡–¡™±Ì£¨∏˘æ›π´ Ωº∆À„![]() £¨∂‘’’ƒø÷–µƒ±Ì∏Ò£¨µ√≥ˆÕ≥º∆Ω·¬€£ª
£¨∂‘’’ƒø÷–µƒ±Ì∏Ò£¨µ√≥ˆÕ≥º∆Ω·¬€£ª
£®3£©œ»«Û≥ˆ∏√µÿ«¯√ø√˚ªº’fl«±∑¸∆⁄≥¨π˝6ÃÏ∑¢…˙µƒ∏≈¬ £¨…˵˜≤ȵƒ10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝Œ™![]() £¨”…”⁄∏√µÿ«¯»À ˝Ωœ∂‡£¨‘Ú
£¨”…”⁄∏√µÿ«¯»À ˝Ωœ∂‡£¨‘Ú![]() Ω¸À∆∑˛¥”∂˛œÓ∑÷≤º£¨º¥
Ω¸À∆∑˛¥”∂˛œÓ∑÷≤º£¨º¥![]() £¨
£¨![]() £¨
£¨![]() °≠£¨10£¨”…
°≠£¨10£¨”…![]() µ√£∫
µ√£∫![]() £¨º¥’‚10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝◊Ó”–ø…ƒ‹ «4»À£Æ
£¨º¥’‚10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝◊Ó”–ø…ƒ‹ «4»À£Æ
Ω‚£∫£®1£©![]() £®ÃÏ£©.
£®ÃÏ£©.
£®2£©∏˘æ›Ã‚“‚£¨≤π≥‰ÕÍ’˚µƒ¡–¡™±Ì»Áœ¬£∫
«±∑¸∆⁄ | «±∑¸∆⁄ | ◊‹º∆ | |
50ÀÍ“‘…œ£®∫¨50ÀÍ£© | 15 | 5 | 20 |
50ÀÍ“‘œ¬ | 9 | 11 | 20 |
◊‹º∆ | 24 | 16 | 40 |
‘Ú![]() £¨
£¨
æ≠≤ọ̇̄¨µ√![]() £¨À˘“‘√ª”–
£¨À˘“‘√ª”–![]() µƒ∞—Œ’»œŒ™«±∑¸∆⁄”Ϊº’flƒÍ¡‰”–πÿ£ª
µƒ∞—Œ’»œŒ™«±∑¸∆⁄”Ϊº’flƒÍ¡‰”–πÿ£ª
£®3£©”…“‚ø…÷™£¨∏√µÿ«¯√ø√˚ªº’fl«±∑¸∆⁄≥¨π˝6ÃÏ∑¢…˙µƒ∏≈¬ Œ™![]() .
.
…˵˜≤ȵƒ10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝Œ™![]() £¨”…”⁄∏√µÿ«¯»À ˝Ωœ∂‡£¨‘Ú
£¨”…”⁄∏√µÿ«¯»À ˝Ωœ∂‡£¨‘Ú![]() Ω¸À∆∑˛¥”∂˛œÓ∑÷≤º£¨º¥
Ω¸À∆∑˛¥”∂˛œÓ∑÷≤º£¨º¥![]() £¨
£¨![]() £¨
£¨![]() °≠£¨10.
°≠£¨10.
”…![]() £¨
£¨
µ√
ªØºÚµ√![]() £¨
£¨
”÷![]() £¨À˘“‘
£¨À˘“‘![]() £¨º¥’‚10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝◊Ó”–ø…ƒ‹ «4»À.
£¨º¥’‚10√˚ªº’fl÷–«±∑¸∆⁄≥¨π˝6Ãϵƒ»À ˝◊Ó”–ø…ƒ‹ «4»À.


 ∂·π⁄ΩæÌ»´ƒ‹¡∑øºœµ¡–¥∞∏
∂·π⁄ΩæÌ»´ƒ‹¡∑øºœµ¡–¥∞∏
| ƒÍº∂ | ∏fl÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏fl“ª | ∏fl“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl∂˛ | ∏fl∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏fl»˝ | ∏fl»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™Œfi«Ó ˝¡–![]() ¬˙◊„£∫
¬˙◊„£∫![]() £¨
£¨![]() £Æ
£Æ
£®¢Ò£©»Ù![]() £ª
£ª
£®¢°£©«Û÷§£∫![]() £ª
£ª
£®¢¢£© ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() «“
«“![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®¢Ú£©»Ù∂‘»Œ“‚µƒ![]() £¨∂º”–
£¨∂º”–![]() £¨–¥≥ˆ
£¨–¥≥ˆ![]() µƒ»°÷µ∑∂Œß≤¢Àµ√˜¿Ì”…£Æ
µƒ»°÷µ∑∂Œß≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚◊∂P©ÅABCD÷–£¨°˜PADŒ™µ»±fl»˝Ω«–Œ£¨AB£ΩAD![]() CD£Ω2£¨°œBAD£Ω°œADC£Ω90°„£¨°œPDC£Ω60°„£¨EŒ™BCµƒ÷–µ„.
CD£Ω2£¨°œBAD£Ω°œADC£Ω90°„£¨°œPDC£Ω60°„£¨EŒ™BCµƒ÷–µ„.
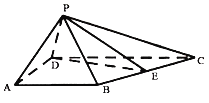
£®1£©÷§√˜£∫AD°ÕPE.
£®2£©«Û÷±œflPA”Î∆Ω√ÊPDEÀ˘≥…Ω«µƒ¥Û–°.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´6∏ˆ ˝2°¢0°¢1°¢9°¢20°¢19∞¥»Œ“‚¥Œ–Ú≈≈≥…“ª––£¨∆¥≥…“ª∏ˆ8Œª ˝( ◊Œª≤ªŒ™0)£¨‘Ú≤˙…˙µƒ≤ªÕ¨µƒ8Œª ˝µƒ∏ˆ ˝Œ™______ .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
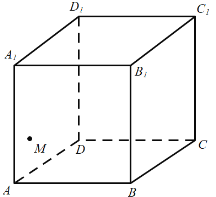
°æƒø°ø»ÁÕº£¨µ„![]() «’˝∑ΩÃÂ
«’˝∑ΩÃÂ![]() ÷–µƒ≤‡√Ê
÷–µƒ≤‡√Ê![]() …œµƒ“ª∏ˆ∂ص„£¨‘Úœ¬¡–Ω·¬€’˝»∑µƒ «£® £©
…œµƒ“ª∏ˆ∂ص„£¨‘Úœ¬¡–Ω·¬€’˝»∑µƒ «£® £©
A.µ„![]() ¥Ê‘⁄Œfi ˝∏ˆŒª÷√¬˙◊„
¥Ê‘⁄Œfi ˝∏ˆŒª÷√¬˙◊„![]()
B.»Ù’˝∑Ωõƒ¿‚≥§Œ™1£¨»˝¿‚◊∂![]() µƒÃª˝◊Ó¥Û÷µŒ™
µƒÃª˝◊Ó¥Û÷µŒ™![]()
C.‘⁄œfl∂Œ![]() …œ¥Ê‘⁄µ„
…œ¥Ê‘⁄µ„![]() £¨ π“Ï√Ê÷±œfl
£¨ π“Ï√Ê÷±œfl![]() ”Î
”Î![]() À˘≥…µƒΩ« «
À˘≥…µƒΩ« «![]()
D.µ„![]() ¥Ê‘⁄Œfi ˝∏ˆŒª÷√¬˙◊„µΩ÷±œfl
¥Ê‘⁄Œfi ˝∏ˆŒª÷√¬˙◊„µΩ÷±œfl![]() ∫Õ÷±œfl
∫Õ÷±œfl![]() µƒæ‡¿Îœ‡µ».
µƒæ‡¿Îœ‡µ».
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øÀƒ¿‚◊∂![]() µƒµ◊√ÊABCD «±fl≥§Œ™aµƒ¡‚–Œ£¨
µƒµ◊√ÊABCD «±fl≥§Œ™aµƒ¡‚–Œ£¨![]() √ÊABCD£¨
√ÊABCD£¨![]() £¨E£¨F∑÷± «CD£¨PCµƒ÷–µ„.
£¨E£¨F∑÷± «CD£¨PCµƒ÷–µ„.

£®1£©«Û÷§£∫∆Ω√Ê![]() ∆Ω√ÊPAB£ª
∆Ω√ÊPAB£ª
£®2£©M «PB…œµƒ∂ص„£¨EM”Î∆Ω√ÊPABÀ˘≥…µƒ◊Ó¥ÛΩ«Œ™![]() £¨«Û∂˛√ÊΩ«
£¨«Û∂˛√ÊΩ«![]() µƒ”‡œ“÷µ.
µƒ”‡œ“÷µ.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘≤![]() π˝Õ÷‘≤
π˝Õ÷‘≤![]() µƒœ¬∂•µ„º∞◊Û°¢”“Ωπµ„
µƒœ¬∂•µ„º∞◊Û°¢”“Ωπµ„![]() £¨
£¨![]() £¨π˝Õ÷‘≤
£¨π˝Õ÷‘≤![]() µƒ◊ÛΩπµ„
µƒ◊ÛΩπµ„![]() µƒ÷±œfl”ÎÕ÷‘≤
µƒ÷±œfl”ÎÕ÷‘≤![]() œ‡Ωª”⁄
œ‡Ωª”⁄![]() £¨
£¨![]() ¡Ωµ„£¨œfl∂Œ
¡Ωµ„£¨œfl∂Œ![]() µƒ÷–¥πœflΩª
µƒ÷–¥πœflΩª![]() ÷·”⁄µ„
÷·”⁄µ„![]() «“¥π◊„Œ™µ„
«“¥π◊„Œ™µ„![]() £Æ
£Æ
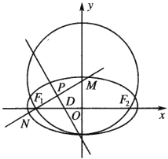
£®¢Ò£©«ÛÕ÷‘≤![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®¢Ú£©÷§√˜£∫µ±÷±œfl![]() –±¬ ±‰ªØ ±
–±¬ ±‰ªØ ±![]() Œ™∂®÷µ£Æ
Œ™∂®÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™’˝œÓ ˝¡–![]() ¬˙◊„£∫
¬˙◊„£∫ ![]() £¨
£¨ ![]() .
.![]() Œ™ ˝¡–
Œ™ ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫Õ.
œÓ∫Õ.
£®¢Ò£©«Û÷§£∫∂‘»Œ“‚’˝’˚ ˝![]() £¨”–
£¨”–![]() £ª
£ª
£®¢Ú£©…Ë ˝¡–![]() µƒ«∞
µƒ«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() £¨«Û÷§£∫∂‘»Œ“‚
£¨«Û÷§£∫∂‘»Œ“‚![]() £¨◊‹¥Ê‘⁄’˝’˚ ˝
£¨◊‹¥Ê‘⁄’˝’˚ ˝![]() £¨ πµ√
£¨ πµ√![]() ±£¨
±£¨ ![]() .
.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏fl÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπ⁄◊¥≤°∂æ «“ª∏ˆ¥Û–Õ≤°∂溓◊£¨“—÷™µƒ”–÷–∂´∫ÙŒ¸◊€∫œ’˜£®MERS£©∫Õ—œ÷ÿº±–‘∫ÙŒ¸◊€∫œ’˜£®SARS£©µ»Ωœ—œ÷ÿµƒº≤≤°£¨–¬–Õπ⁄◊¥≤°∂森nCoV£© «“‘«∞¥”Œ¥‘⁄»ÀÃÂ÷–∑¢œ÷µƒπ⁄◊¥≤°∂æ–¬∂æ÷Í£¨ƒ≥–°«¯Œ™Ω¯“ª≤Ω◊ˆ∫√–¬–Õπ⁄◊¥≤°∂æ∑Œ—◊“fl«È÷™ ∂µƒΩÔ˝£¨‘⁄–°«¯ƒ⁄ø™’π°∞–¬–Õπ⁄◊¥≤°∂æ∑¿“fl∞≤»´π´“ÊøŒ°±‘⁄œfl—ßœ∞£¨‘⁄¥À÷Æ∫Û◊È÷Ø¡À°∞–¬–Õπ⁄◊¥≤°∂æ∑¿“fl∞≤»´÷™ ∂æ∫»¸°±‘⁄œflªÓ∂أƓ—÷™Ω¯»Î戻¸µƒ∑÷± «º◊°¢““°¢±˚°¢∂°ÀƒŒª“µ÷˜£¨æˆ»¸∫ÛÀƒŒª“µ÷˜œ‡”¶µƒ√˚¥ŒŒ™µ⁄1£¨2£¨3£¨4√˚£¨∏√–°«¯Œ™¡À÷∏fl“µ÷˜√«µƒ≤Œ”Î∂»∫Õ÷ÿ ”∂»£¨—˚«Î–°«¯ƒ⁄µƒÀ˘”–“µ÷˜‘⁄±»»¸Ω· ¯«∞∂‘ÀƒŒª“µ÷˜µƒ√˚¥ŒΩ¯––‘§≤‚£¨»Ù‘§≤‚ÕÍ»´’˝»∑Ω´ª·ªÒµ√¿Ò∆∑£¨œ÷”√a£¨b£¨c£¨d±Ì æƒ≥“µ÷˜∂‘º◊°¢““°¢±˚°¢∂°ÀƒŒª“µ÷˜µƒ√˚¥Œ◊ˆ≥ˆ“ª÷÷µ»ø…ƒ‹µƒ‘§≤‚≈≈¡–£¨º«X£Ω|a©Å1|+|b©Å2|+|c©Å3|+|d©Å4|£Æ
£®1£©«Û∏√“µ÷˜ªÒµ√¿Ò∆∑µƒ∏≈¬ £ª
£®2£©«ÛXµƒ∑÷≤º¡–º∞ ˝—ß∆⁄Õ˚£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒfi÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com