
【题目】函数![]() 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)写出![]() 及图中
及图中![]() 的值.
的值.
(Ⅱ)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.

【答案】(Ⅰ)![]() ,
, ![]() .(Ⅱ)最大值
.(Ⅱ)最大值![]() ,最小值
,最小值![]() .
.
【解析】试题分析:(1)将点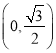 代入,由已给条件可求得
代入,由已给条件可求得![]() ;由
;由![]() 并结合图象可求得
并结合图象可求得![]() .
.
(2)由(1)可得到![]() ,由
,由![]() ,得
,得![]() ,可得在
,可得在![]() 和
和![]() 时,函数
时,函数![]() 分别取得最大值和最小值。
分别取得最大值和最小值。
试题解析:(Ⅰ)∵图象过点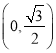 ,∴
,∴![]() ,
,
又![]() ,∴
,∴![]() ,
,
由![]() ,得
,得![]() 或
或![]() ,
, ![]() ,
,
又![]() 的周期为
的周期为![]() ,结合图象知
,结合图象知![]() ,∴
,∴![]() .
.
(Ⅱ)由题意可得![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() ,
,
当![]() ,即
,即![]() 时,
时, ![]() 取得最小值
取得最小值![]() .
.
点睛: 三角函数式的化简要遵循“三看”原则
(1)一看“角”,这是最重要的一环,通过看角之间的区别和联系,把角进行合理的拆分,从而正确使用公式;
(2)而看“函数名称”看函数名称之间的差异,从而确定使用公式,常见的有“切化弦”;
(3)三看“结构特征”,分析结构特征,可以帮助我们找到变形的方向,如“遇到分式通分”等.


 作业辅导系列答案
作业辅导系列答案科目:高中数学 来源: 题型:
【题目】如图,在圆内画1条线段,将圆分割成两部分;画2条相交线段,彼此分割成4条线段,将圆分割成4部分;画3条线段,彼此最多分割成9条线段,将圆最多分割成7部分;画4条线段,彼此最多分割成16条线段,将圆最多分割成11部分.那么




(1)在圆内画5条线段,它们彼此最多分割成多少条线段?将圆最多分割成多少部分?
(2)猜想:圆内两两相交的n条线段,彼此最多分割成多少条线段?
(3)猜想:在圆内画n条线段,两两相交,将圆最多分割成多少部分?
并用数学归纳法证明你所得到的猜想.
查看答案和解析>>
科目:高中数学 来源: 题型:
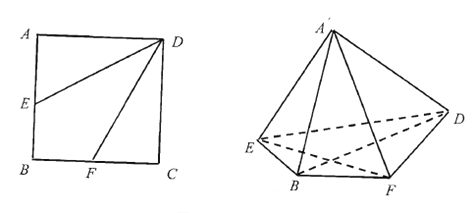
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,将
的中点,将![]() ,
, ![]() ,分别沿
,分别沿![]() ,
, ![]() 折起,使
折起,使![]() ,
, ![]() 两点重合于点
两点重合于点![]() ,连接
,连接![]() .
.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com