
【题目】圆x2+y2=1上任意一点P,过点P作两直线分别交圆于A,B两点,且∠APB=60°,则|PA|2+|PB|2的取值范围为___.
科目:高中数学 来源: 题型:
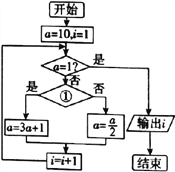
【题目】1927年德国汉堡大学的学生考拉兹提出一个猜想:对于每一个正整数,如果它是奇数,对它乘3再加1,如果它是偶数,对它除以2,这样循环,最终结果都能得到1.该猜想看上去很简单,但有的数学家认为“该猜想任何程度的解决都是现代数学的一大进步,将开辟全新的领域至于如此简单明了的一个命题为什么能够开辟一个全新的领域,这大概与它其中蕴含的奇偶归一思想有关.如图是根据考拉兹猜想设计的一个程序框图,则①处应填写的条件及输出的结果![]() 分别为
分别为
A. ![]() 是偶数?;6 B.
是偶数?;6 B. ![]() 是偶数?;8
是偶数?;8
C. ![]() 是奇数?;5 D.
是奇数?;5 D. ![]() 是奇数?;7
是奇数?;7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设平面直角坐标系xOy中,曲线G:y= ![]() +
+ ![]() x﹣a2(x∈R),a为常数.
x﹣a2(x∈R),a为常数.
(1)若a≠0,曲线G的图象与两坐标轴有三个交点,求经过这三个交点的圆C的一般方程;
(2)在(1)的条件下,求圆心C所在曲线的轨迹方程;
(3)若a=0,已知点M(0,3),在y轴上存在定点N(异于点M)满足:对于圆C上任一点P,都有 ![]() 为一常数,试求所有满足条件的点N的坐标及该常数.
为一常数,试求所有满足条件的点N的坐标及该常数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() =(2sinx,cosx+sinx),
=(2sinx,cosx+sinx), ![]() =(cosx,cosx﹣sinx),f(x)=
=(cosx,cosx﹣sinx),f(x)= ![]()
![]() .
.
(1)求函数f(x)的单调区间;
(2)若关于x的方程f(x)﹣m=0(m∈R)在区间(0, ![]() )内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
)内有两个不相等的实数根x1 , x2 , 记t=mcos(x1+x2),求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=﹣3x2+a(6﹣a)x+b,a,b为实数.
(1)当b=﹣6时,解关于a的不等式f(1)>0;
(2)若不等式f(x)>0的解集为(﹣1,3),求实数a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将圆x2+y2=1 每一点的,横坐标保持不变,纵坐标变为原来的2倍,得到曲线C.
(1)写出C的参数方程;
(2)设直线l:2x+y-2=0 与C的交点为P1,P2 ,以坐标原点为极点, x 轴的正半轴为极轴建立极坐标系,求线段 P1P2 的中点且与 l 垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}中,a1=1,Sn是数列{an}的前n项和,对任意n∈N* , 有2Sn=2pan2+pan﹣p(p∈R)
(1)求常数p的值;
(2)求数列{an}的通项公式;
(3)记bn= ![]() ,求数列{bn}的前n项和T.
,求数列{bn}的前n项和T.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合是“好集合”.给出下列4个集合:①
成立,则称集合是“好集合”.给出下列4个集合:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“好集合”的序号是( )
.其中为“好集合”的序号是( )
A. ①②④ B. ②③ C. ③④ D. ①③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com