
【题目】某运动会将在深圳举行,组委会招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:![]() ),身高在
),身高在![]() 以上(包括
以上(包括![]() )定义为“高个子”,身高在
)定义为“高个子”,身高在![]() 以下(不包括
以下(不包括![]() )定义为“非高个子”.
)定义为“非高个子”.
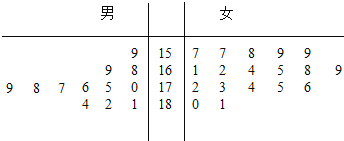
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率;
(2)若从身高![]() 以上(包括
以上(包括![]() )的志愿者中选出男、女各一人,设这2人身高相差
)的志愿者中选出男、女各一人,设这2人身高相差![]() (
(![]() ),求
),求![]() 的分布列和数学期望(均值).
的分布列和数学期望(均值).
 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】为了解某地区足球特色学校的发展状况,某调查机构得到如下统计数据:
年份x | 2014 | 2015 | 2016 | 2017 | 2018 |
足球特色学校y(百个) | 0.30 | 0.60 | 1.00 | 1.40 | 1.70 |
(1)根据上表数据,计算y与x的相关系数r,并说明y与x的线性相关性强弱(已知:![]() 则认为
则认为![]() 与
与![]() 线性相关性很强;
线性相关性很强;![]() ,则认为
,则认为![]() 与
与![]() 线性相关性一般,
线性相关性一般,![]() ,则认为y与x线性相关性较弱)
,则认为y与x线性相关性较弱)
(2)求y与x的线性回归方程,并预测该地区2019年足球特色学校的个数(精确到个位)
参考公式:
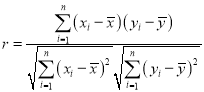
![]() ;
;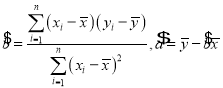
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线![]() 的参数方程为
的参数方程为![]() ,
,![]() 为参数
为参数![]() ,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线
,在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
![]() 求曲线
求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
![]() 若射线l:
若射线l:![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为A,
的交点分别为A,![]() B异于原点
B异于原点![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如上图.现在图(3)中随机选取一个点,则此点取自阴影部分的概率为________

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下边的折线图给出的是甲、乙两只股票在某年中每月的收盘价格,已知股票甲的极差是6.88元,标准差为2.04元;股票乙的极差为27.47元,标准差为9.63元,根据这两只股票在这一年中的波动程度,给出下列结论:①股票甲在这一年中波动相对较小,表现的更加稳定;②购买股票乙风险高但可能获得高回报;③股票甲的走势相对平稳,股票乙的股价波动较大;④两只般票在全年都处于上升趋势.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() .
.
(1)求椭圆![]() 的方程,并求其离心率;
的方程,并求其离心率;
(2)过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,设点
,设点![]() 为第四象限内一点且在椭圆
为第四象限内一点且在椭圆![]() 上(点
上(点![]() 不在直线
不在直线![]() 上),点
上),点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与
与![]() 交于另一点
交于另一点![]() .设
.设![]() 为原点,判断直线
为原点,判断直线![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①正切函数图象的对称中心是唯一的;
②若函数![]() 的图像关于直线
的图像关于直线![]() 对称,则这样的函数
对称,则这样的函数![]() 是不唯一的;
是不唯一的;
③若![]() ,
,![]() 是第一象限角,且
是第一象限角,且![]() ,则
,则![]() ;
;
④若![]() 是定义在
是定义在![]() 上的奇函数,它的最小正周期是
上的奇函数,它的最小正周期是![]() ,则
,则![]() .
.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com