设三次函数f(x)＝ax3＋bx2＋cx＋d(a＜b＜c)，在x＝1处取得极值，其图象在x＝m处的切线的斜率为－3a．
(Ⅰ)求证：
；
(Ⅱ)若函数y＝f(x)在区间[s，t]上单调递增，求|s－t|的取值范围；
(Ⅲ)问是否存在实数k(k是与a，b，c，d无关的常数)，当x≥k时，恒有
恒成立？若存在，试求出k的最小值；若不存在，请说明理由．
|
解：(Ⅰ)方法一、 ∵ 由①代入②得 得 将 由③、④得 方法二、同上可得： 将(1)变为： 所以 方法三：同上可得： 可得： 因为 由韦达定理得 所以： 方法四：由 (Ⅱ)由(Ⅰ)知， ∴方程 又 ∴当 ∴函数 由 ∵函数 即 (Ⅲ)由 ∵ ∴ 由题意，得 ∴存在实数 |
名校课堂系列答案科目：高中数学 来源：内蒙古呼伦贝尔市牙克石林业一中2012届高三上学期第二次模拟考试数学文科试题 题型：013
设三次函数f(x)的导函数为
(x)，函数y＝x·(x)的图象的一部分如图所示，则
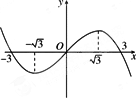
f
(x)的极大值为f(
)，极小值为f(－)
f
(x)的极大值为f(－)，极小值为f()
f
(x)的极大值为f(－3)，极小值为f(3)f
(x)的极大值为f(3)，极小值为f(－3)查看答案和解析>>
科目：高中数学 来源：广东省珠海一中2012届高三高考模拟数学文科试题 题型：022
对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，定义：设
是函数y＝f(x)的导数y＝
的导数，若方程
＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．”
请你将这一发现为条件，函数
，则它的对称中心为________；
计算
＝________．
查看答案和解析>>
科目：高中数学 来源：安徽省蚌埠市2009届高三上学期第一次教学质量模拟考试、数学(理) 题型：044
设三次函数f(x)＝ax3＋bx2＋cx＋d(a＜b＜c)，在x＝1处取得极值，其图像在x＝m处的切线的斜率为－3a．
(1)求证：
；
(2)若函数y＝f(x)在区间[s，t]上单调递增，求|s－t|的取值范围；
(3)问是否存在实数k(k是与a，b，c，d无关的常数)，当x≥k时，恒有
恒成立？若存在，试求出k的最小值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源：2011-2012学年江西省高三第一次月考理科数学试卷 题型：填空题
对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，定义：设f″(x)是函数y＝f(x)的导数y＝f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．有同学发现“任何一个三次函数都有‘拐点’；任何一个三次函数都有对称中心；且‘拐点’就是对称中心．如“函数f(x)＝x3－3x2＋3x对称中心为点 (1,1)”请你将这一发现
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
．由题设，得
①
②
，∴
，∴
．
，∴
，
∴
或
③
代入
中，得
④
；
代入(2)可得：
，
，则
代入(2)
，显然
，所以
，
，所以
，即
，则
，由
且
，由此可知
的判别式Δ＝
有两个不等的实根
，
，∴
，
或
时，
，当
时，
，
的单调增区间是
，∴
，
．
在区间
上单调递增，∴
，∴
，
的取值范围是
；
，即
，
，
，
或
．
，∴
，
满足条件，即
．