
| 甲 | | 乙 |
| 6 4 3 | 9 | 1 5 |
| 8 7 7 5 4 2 | 8 | 0 1 3 6 6 8 8 9 |
| 9 | 7 | |
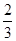 .
.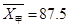 ,
,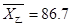 ,
,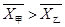 ,所以甲演唱水平更高一点,但甲的方差较大,即评委对甲的水平认可存在较大的差异 5分
,所以甲演唱水平更高一点,但甲的方差较大,即评委对甲的水平认可存在较大的差异 5分
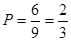 . 12分
. 12分

科目:高中数学 来源:不详 题型:解答题

| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
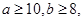 求数学成绩为优秀的人数比及格的人数少的概率.
求数学成绩为优秀的人数比及格的人数少的概率.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
,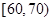 ,
,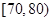 ,
,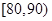 ,
,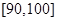 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在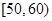 ,
,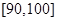 的数据)
的数据)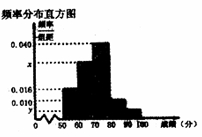
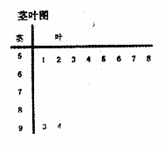
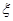 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在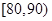 的学生个数,求
的学生个数,求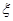 的分布列及其数学期望
的分布列及其数学期望 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 选择题 | 40 | 55 | 50 | 45 | 50 | 40 | 45 | 60 | 40 |
| 填空题 | 12 | 16 | 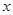 | 12 | 16 | 12 | 8 | 12 | 8 |
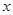 的值及他们填空题得分的标准差;
的值及他们填空题得分的标准差;查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
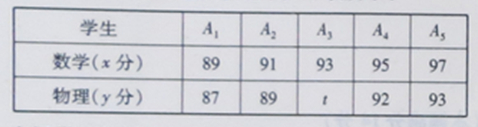
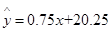 ,那么表中t的值为 .
,那么表中t的值为 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 年龄 (岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频 数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成 人数 | 4 | 8 | 9 | 6 | 4 | 3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 月收入 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75] |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 非高收入族 | 高收入族 | 合计 |
| 赞成 | | | |
| 不赞成 | | | |
| 合计 | | | |

| P(K2≥k0) | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.24 | B.8 | C.10 | D.12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com