
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,Q为BB1的中点,过A1 , Q,D三点的平面记为α. 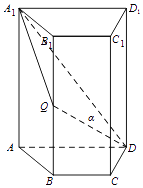
(1)证明:平面α与平面A1B1C1D1的交线平行于直线CD;
(2)若AA1=3,BC=CD= ![]() ,∠BCD=120°,求平面α与底面ABCD所成二面角的大小.
,∠BCD=120°,求平面α与底面ABCD所成二面角的大小.
【答案】
(1)证明:如图,延长AB,DC交于点P,
∵AD∥BC,且AD=2BC,∴AB=BP,
又∵Q为BB1的中点,
∴A1,Q,P三点共线,此时平面α与平面ABCD的交线为CD,
又平面ABCD∥平面A1B1C1D1,根据面面平行的性质定理可得,
平面α与平面A1B1C1D1的交线平行于直线CD;
(2)解:在梯形ABCD中,∵BC=CD= ![]() ,∠BCD=120°,
,∠BCD=120°,
∴BD=3, ![]() ,
, ![]() ,得
,得 ![]() ,
, ![]() ,
,
说明梯形ABCD是等腰梯形,
∴AC=BD=3,
可知△ADP为等边三角形,连接AC、A1C,则AC⊥CD,
又AA1⊥CD,∴CD⊥平面AA1C,
此时∠A1CA就是平面α与底面ABCD所成二面角的平面角,
在直角△A1CA中,AC=AA1=3,∴ ![]() ,
,
即平面α与底面ABCD所成二面角的大小为 ![]() .
.

【解析】(1)延长AB,DC交于点P,由已知可得AD∥BC,且AD=2BC,则AB=BP,得到A1,Q,P三点共线,此时平面α与平面ABCD的交线为CD,再由面面平行的性质可得平面α与平面A1B1C1D1的交线平行于直线CD;(2)在梯形ABCD中,由已知求得ABCD是等腰梯形,进一步得到△ADP为等边三角形,连接AC、A1C,则AC⊥CD,可得∠A1CA就是平面α与底面ABCD所成二面角的平面角,在直角△A1CA中,求得 ![]() ,即平面α与底面ABCD所成二面角的大小为
,即平面α与底面ABCD所成二面角的大小为 ![]() .
.
【考点精析】解答此题的关键在于理解平面与平面平行的判定的相关知识,掌握判断两平面平行的方法有三种:用定义;判定定理;垂直于同一条直线的两个平面平行.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在考试测评中,常用难度曲线图来检测题目的质量,一般来说,全卷得分高的学生,在某道题目上的答对率也应较高,如果是某次数学测试压轴题的第1、2问得分难度曲线图,第1、2问满分均为6分,图中横坐标为分数段,纵坐标为该分数段的全体考生在第1、2问的平均难度,则下列说法正确的是( ) 
A.此题没有考生得12分
B.此题第1问比第2问更能区分学生数学成绩的好与坏
C.分数在[40,50)的考生此大题的平均得分大约为4.8分
D.全体考生第1问的得分标准差小于第2问的得分标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,M为C上除长轴顶点外的一动点,以M为圆心,
,M为C上除长轴顶点外的一动点,以M为圆心, ![]() 为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB=
为半径作圆,过原点O作圆M的两条切线,A、B为切点,当M为短轴顶点时∠AOB= ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)设椭圆的右焦点为F,过点F作MF的垂线交直线x= ![]() a于N点,判断直线MN与椭圆的位置关系.
a于N点,判断直线MN与椭圆的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且2Sn=4an﹣1. (Ⅰ)求{an}的通项公式;
(Ⅱ)设bn=anan+1﹣2,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[17.5,30],样本数据分组为[17.5,20),[20,22.5),[22.5,25),[25,27.5),[27.5,30].根据直方图,若这200名学生中每周的自习时间不超过m小时的人数为164,则m的值约为( ) 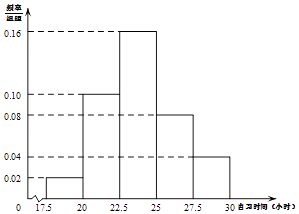
A.26.25
B.26.5
C.26.75
D.27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名篮球运动员在7场比赛中的得分情况如茎叶所示, ![]() 甲、
甲、 ![]() 乙分别表示甲、乙两人的平均得分,则下列判断正确的是( )
乙分别表示甲、乙两人的平均得分,则下列判断正确的是( ) 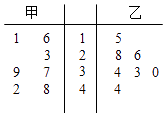
A.![]() 甲>
甲> ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
B.![]() 甲>
甲> ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
C.![]() 甲<
甲< ![]() 乙 , 甲比乙得分稳定
乙 , 甲比乙得分稳定
D.![]() 甲<
甲< ![]() 乙 , 乙比甲得分稳定
乙 , 乙比甲得分稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体是由一个直平行六面体被平面AEFG所截后得到的,其中∠BAE=∠GAD=45°,AB=2AD=2,∠BAD=60°. 
(1)求证:BD⊥平面ADG;
(2)求此多面体的全面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10支队伍参加篮球比赛,规定:比赛采取单循环比赛制,即每支队伍与其他9支队伍各比赛一场;每场比赛中,胜方得2分,负方得0分,平局双方各得1分.下面关于这10支队伍得分的叙述正确的是( )
A.可能有两支队伍得分都是18分
B.各支队伍得分总和为180分
C.各支队伍中最高得分不少于10分
D.得偶数分的队伍必有偶数个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com