
【题目】已知平面上三个向量 ![]() 的模均为1,它们相互之间的夹角均为120°.
的模均为1,它们相互之间的夹角均为120°.
(1)求证: ![]() ;
;
(2)若|k ![]() |>1 (k∈R),求k的取值范围.
|>1 (k∈R),求k的取值范围.
【答案】
(1)证明∵ ![]() =
= ![]() =|
=| ![]() ||
|| ![]() |cos120°﹣|
|cos120°﹣| ![]() ||
|| ![]() |cos120°=0,
|cos120°=0,
∴ ![]()
(2)解:|k ![]() |>1
|>1 ![]() >1,
>1,
即 ![]()
![]() >1.
>1.
∵| ![]() |=|
|=| ![]() |=|
|=| ![]() |=1,且
|=1,且 ![]() 相互之间的夹角均为120°,
相互之间的夹角均为120°,
∴ ![]() =1,
=1, ![]() =﹣
=﹣ ![]() ,
,
∴k2+1﹣2k>1,即k2﹣2k>0,
∴k>2或k<0
【解析】(1)利用向量的分配律及向量的数量积公式求出 ![]() ;利用向量的数量积为0向量垂直得证.(2)利用向量模的平方等于向量的平方及向量的数量积公式将已知等式平方得到关于k的不等式求出k的范围.
;利用向量的数量积为0向量垂直得证.(2)利用向量模的平方等于向量的平方及向量的数量积公式将已知等式平方得到关于k的不等式求出k的范围.
【考点精析】关于本题考查的数量积判断两个平面向量的垂直关系,需要了解若平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证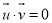 ;即:两平面垂直
;即:两平面垂直![]() 两平面的法向量垂直才能得出正确答案.
两平面的法向量垂直才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(I)若曲线![]() 在点
在点![]() 处的切线平行于
处的切线平行于![]() 轴,求
轴,求![]() 的值;
的值;
(II)求函数![]() 的极值;
的极值;
(III)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=log2an,Tn为{bn}的前n项和,求证![]() <2.
<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax3+bx2+cx+d(a、b、c、d∈R)满足:x∈R都有f(x)+f(﹣x)=0,且x=1时,f(x)取极小值![]() .
.
(1)f(x)的解析式;
(2)当x∈[﹣1,1]时,证明:函数图象上任意两点处的切线不可能互相垂直:
(3)设F(x)=|xf(x)|,证明: ![]() 时,
时, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队参加听歌猜歌名游戏,每队3人.随机播放一首歌曲,参赛者开始抢答,每人只有一次抢答机会(每人抢答机会均等),答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为 ![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为 ![]() ,
, ![]() ,
, ![]() ,且各人回答正确与否相互之间没有影响.
,且各人回答正确与否相互之间没有影响.
(Ⅰ)若比赛前随机从两队的6个选手中抽取两名选手进行示范,求抽到的两名选手在同一个队的概率;
(Ⅱ)用ξ表示甲队的总得分,求随机变量ξ的分布列和数学期望;
(Ⅲ)求两队得分之和大于4的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足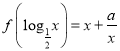 为常数
为常数
(1)求函数f(x)的表达式;
(2)如果f(x)为偶函数,求a的值;
(3)当f(x)为偶函数时,若方程f(x)=m有两个实数根x1,x2;其中x1<0,0<x2<1;求实数m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古代中国数学辉煌灿烂,在《张丘建算经》中记载:“今有十等人,大官甲等十人官赐金,以等次差降之.上三人先入,得金四斤持出;下四人后入,得金三斤持出;中央三人未到者,亦依等次更给.问:各得金几何及未到三人复应得金几何?”则该问题中未到三人共得金多少斤?( )
A.![]()
B.![]()
C.2
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com