
【题目】已知函数f(x)=(a﹣1)(ax﹣a﹣x)(0<a<1).
(1)判断f(x的奇偶性;
(2)用定义证明f(x)为R上的增函数.
【答案】
(1)解:由函数f(x)=(a﹣1)(ax﹣a﹣x),
对任意x∈R,都有f(﹣x)=(a﹣1)(a﹣x﹣ax)=﹣f(x),
所以f(x)为定义域R上的奇函数;
(2)证明:设x1、x2∈R且x1<x2,则
f(x1)﹣f(x2)=(a﹣1)( ![]() ﹣
﹣ ![]() )﹣(a﹣1)(
)﹣(a﹣1)( ![]() ﹣
﹣ ![]() )
)
=(a﹣1)[( ![]() ﹣
﹣ ![]() )﹣(
)﹣( ![]() ﹣
﹣ ![]() )]
)]
=(a﹣1)[( ![]() ﹣
﹣ ![]() )﹣
)﹣ ![]() ]
]
=(a﹣1)( ![]() ﹣
﹣ ![]() )(1+
)(1+ ![]() ),
),
由于0<a<1, ![]() ﹣
﹣ ![]() >0,1+
>0,1+ ![]() >0,
>0,
于是f(x1)<f(x2),所以f(x)为R上的增函数
【解析】(1)利用奇偶性的定义即可判断函数f(x)为定义域上的奇函数;(2)利用单调性的定义即可证明f(x)为定义域上的增函数.
【考点精析】利用函数单调性的判断方法和函数的奇偶性对题目进行判断即可得到答案,需要熟知单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)对于一切实数x,y均有f(x+y)﹣f(y)=x(x+2y+1)成立,且f(1)=0,则当x∈(0, ![]() ),不等式f(x)+2<logax恒成立时,实数a的取值范围是
),不等式f(x)+2<logax恒成立时,实数a的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法正确的是( )
①函数f(x)的定义域是R,则“x∈R,f(x+1)>f(x)”是“函数f(x)为增函数”的充要条件
②命题“x∈R,( ![]() )x>0”的否定是“x∈R,(
)x>0”的否定是“x∈R,( ![]() )x≤0”
)x≤0”
③命题“若x=2,则x2﹣3x+2=0”的逆否命题是“若x2﹣3x+2≠0,则x≠2”
④p:在△ABC中,若cos2A=cos2B,则A=B;q:y=sinx在第一象限是增函数.则p∧q为真命题.
A.①②③④
B.①③
C.①③④
D.③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若存在闭区间[a,b]D,使得函数f(x)满足:
①f(x)在[a,b]上是单调函数;
②f(x)在[a,b]上的值域是[2a,2b],则称区间[a,b]是函数f(x)的“和谐区间”.
下列结论错误的是( )
A.函数f(x)=x2(x≥0)存在“和谐区间”
B.函数f(x)=2x(x∈R)存在“和谐区间”
C.函数f(x)= ![]() (x>0)不存在“和谐区间”
(x>0)不存在“和谐区间”
D.函数f(x)=log2x(x>0)存在“和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=x2﹣x+b,且f(log2a)=b,log2f(a)=2(a>0且a≠1),
(1)求a,b;
(2)求f(log2x)的最小值及相应 x的值;
(3)若f(log2x)>f(1)且log2f(x)<f(1),求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为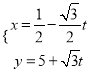 (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立坐标系.
轴的正半轴为极轴建立坐标系.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)射线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,与曲线
,与曲线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若圆C的半径为1,圆心在第一象限,且与直线4x-3y=0和x轴都相切,则该圆的标准方程是( )
A.(x-2)2+(y-1)2=1
B.(x-2)2+(y-3)2=1
C.(x-3)2+(y-2)2=1
D.(x-3)2+(y-1)2=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com