
【题目】已知函数![]() .
.
![]() 若
若![]() ,
,![]() ,试证明:当
,试证明:当![]() 时,
时,![]() ;
;
![]() 若对任意
若对任意![]() ,
,![]() 均有两个极值点
均有两个极值点![]() ,
,![]()
![]() 试求b应满足的条件;
试求b应满足的条件;
![]() 当
当![]() 时,证明:
时,证明:![]() .
.
【答案】(1)见解析(2)![]() ,
,![]() .见解析
.见解析
【解析】
(1)求出导数![]() ,求出其最小值,由最小值大于0,从而证明出结论.
,求出其最小值,由最小值大于0,从而证明出结论.
(2)![]() 首先
首先![]() =0有两个不等的实根,再用导数研究
=0有两个不等的实根,再用导数研究![]() 的性质,求导
的性质,求导![]() ,利用
,利用![]() 的正负确定
的正负确定![]() 的单调性及最小值点,在
的单调性及最小值点,在![]() 时,计算出
时,计算出![]()
![]() ,由零点存在定理可得
,由零点存在定理可得![]() 存在两个零点,即
存在两个零点,即![]() 有两个极值点;当
有两个极值点;当![]() 时,可取
时,可取![]() ,此时
,此时![]() 没有零点极值点;
没有零点极值点;
![]() 由
由![]() 知,
知,![]() ,
,![]() 为
为![]() 的两个实数根,由于
的两个实数根,由于![]() ,可判断出两零点一正一负,即
,可判断出两零点一正一负,即![]() ,且
,且![]() 在
在![]() 递减,为证题中不等式,先做一些准备工作,下面先证
递减,为证题中不等式,先做一些准备工作,下面先证![]() ,只需证明
,只需证明![]() ,注意到
,注意到![]() 得
得![]() ,从而
,从而![]() ,下面再用导数的知识证明
,下面再用导数的知识证明![]() ;由函数单调性得
;由函数单调性得![]() ,问题转化为只需证明
,问题转化为只需证明![]() ,
,
即证明![]() ,这再用导数加以证明.
,这再用导数加以证明.
![]() 证明:
证明:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() .
.
可得:![]() 时,函数
时,函数![]() 取得极小值即最小值,
取得极小值即最小值,
![]() ,
,
![]() 函数
函数![]() 在当
在当![]() 时单调递增,
时单调递增,![]() .
.
![]() 当
当![]() 时,
时,![]() .
.
![]() ,
,![]() .
.
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
故![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
故![]() 至多有2个零点;
至多有2个零点;
![]() 当
当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
又![]() ,
,
由![]() 可知
可知![]() ,
,
![]() 是R上的连续函数,
是R上的连续函数,
![]() 在
在![]() ,
,![]() 上各有1个零点
上各有1个零点![]() ,
,![]() ,
,
此时,![]() ,
,![]() 为函数
为函数![]() 的2个不同的极值点,
的2个不同的极值点,
故![]() 符合题意;
符合题意;
![]() 当
当![]() 时,取
时,取![]() ,则
,则![]() 在
在![]() 递减,在
递减,在![]() 递增,
递增,
故![]() ,
,
故![]() 时,
时,![]() ,
,
故函数![]() 递增,没有极值点,不合题意,
递增,没有极值点,不合题意,
综上,当![]() 时,对任意
时,对任意![]() ,
,![]() 均有2个极值点;
均有2个极值点;
![]() 由
由![]() 知,
知,![]() ,
,![]() 为
为![]() 的两个实数根,
的两个实数根,
![]() ,
,![]() ,
,![]() 在
在![]() 递减,
递减,
下面先证![]() ,只需证明
,只需证明![]() ,
,
![]() 得
得![]() ,
,
![]() ,
,
设![]() ,
,![]() ,
,
则![]() ,
,
故![]() 在
在![]() 递减,
递减,
![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() 时,
时,![]() ,
,
![]() 在
在![]() 递减,
递减,![]() ,
,
问题转化为只需证明![]() ,
,
即证明![]() ,
,
设函数![]() ,
,![]() ,
,
则![]() ,
,
设![]() ,则
,则![]() ,
,
![]() 在
在![]() 递增,
递增,
![]() ,即
,即![]() ,
,
![]() 在
在![]() 递增,
递增,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,
,
![]() .
.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】一汽车厂生产![]() ,
,![]() ,
,![]() 三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有
三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有![]() 类轿车10辆.
类轿车10辆.
轿车 | 轿车 | 轿车 | |
舒适型 | 100 | 150 |
|
标准型 | 300 | 450 | 600 |
(1)求![]() 的值;
的值;
(2)用分层抽样的方法在![]() 类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从![]() 类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数
类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2 把这8辆轿车的得分看作一个总体,从中任取一个得分数![]() ,记这8辆轿车的得分的平均数为
,记这8辆轿车的得分的平均数为![]() ,定义事件
,定义事件![]() ,且函数
,且函数![]() 没有零点
没有零点![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f1(x),y=f2(x),定义函数f(x)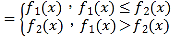 .
.
(1)设函数f1(x)=x+3,f2(x)=x2﹣x,求函数y=f(x)的解析式;
(2)在(1)的条件下,g(x)=mx+2(m∈R),函数h(x)=f(x)﹣g(x)有三个不同的零点,求实数m的取值范围;
(3)设函数f1(x)=x2﹣2,f2(x)=|x﹣a|,函数F(x)=f1(x)+f2(x),求函数F(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于正整数集合![]() ,如果任意去掉其中一个元素
,如果任意去掉其中一个元素![]() 之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合
之后,剩余的所有元素组成的集合都能分为两个交集为空集的集合,且这两个集合的所有元素之和相等,就称集合![]() 为“可分集合”.
为“可分集合”.
(1)判断集合![]() 和
和![]() 是否是“可分集合”(不必写过程);
是否是“可分集合”(不必写过程);
(2)求证:五个元素的集合![]() 一定不是“可分集合”;
一定不是“可分集合”;
(3)若集合![]() 是“可分集合”.
是“可分集合”.
①证明:![]() 为奇数;
为奇数;
②求集合![]() 中元素个数的最小值.
中元素个数的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某亲子公园拟建议广告牌,将边长为![]() 米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等
米的正方形ABCD和边长为1米的正方形AEFG在A点处焊接,AM、AN、GM、DN均用加强钢管支撑,其中支撑钢管GM、DN垂直于地面于M点和N点,且GM、DN、MN长度相等![]() 不计焊接点大小
不计焊接点大小![]()

![]() 若
若![]() 时,求焊接点A离地面距离;
时,求焊接点A离地面距离;
![]() 若记
若记![]() ,求加强钢管AN最长为多少?
,求加强钢管AN最长为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线E上任一点P到直线l:x=4的距离是点P到点M(1,0)的距离的2倍.
(1)求曲线E的方程;
(2)过点A(2,0)作两条互相垂直的直线分别交曲线E于B、D两点(均异于点A),又C(-2,0),求四边形ABCD的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“数学发展史”知识测验后,甲、乙、丙三人对成绩进行预测:
甲说:我的成绩比乙高;
乙说:丙的成绩比我和甲的都高;
丙说:我的成绩比乙高.
成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人中预测正确的是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com