
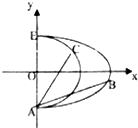
 已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲线C2:x2+y2=r2(x≥0)都过点A(0,-1),且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$
已知曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,x≥0)和曲线C2:x2+y2=r2(x≥0)都过点A(0,-1),且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$分析 (1)由已知曲线都过点A(0,-1),且曲线C1所在的圆锥曲线的离心率为$\frac{\sqrt{3}}{2}$,可确定相应几何量,从而可得曲线C1和曲线C2的方程;
(2)①将直线AB,AC的方程分别与椭圆、圆联立,进而可求点B,C的坐标,从而可得直线BC的方程,进而可知过定点,
②由|$\overrightarrow{BC}$|•|$\overrightarrow{BE}$|=|$\overrightarrow{BC}$•$\overrightarrow{BE}$|,再|根据向量的坐标运算和向量的数量积和基本不等式即可求出.
解答 解:(1)由已知得r2=1,b2=1,
又e=$\frac{c}{a}$=$\frac{\sqrt{{a}^{2}-1}}{a}$=$\frac{\sqrt{3}}{2}$,解得a2=4,
∴曲线C1的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$,(x≥0),
曲线C2的方程为x2+y2=1,(x≥0).
(2)①将y=k1x-1代入$\frac{{x}^{2}}{4}+{y}^{2}=1$,得(1+4k12)x2-8k1x=0,
设A(x1,y1),B(x2,y2),则x1=0,x2=$\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$,
∴B($\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$,$\frac{4{{k}_{1}}^{2}-1}{1+4{{k}_{1}}^{2}}$),
将y=k2x-1代入x2+y2=1,得(1+k22)x2-2k2x=0,
设C(x3,y3),则x3=$\frac{2{k}_{2}}{{{k}_{2}}^{2}+1}$,y3=k2x3-1=$\frac{{{k}_{2}}^{2}-1}{{{k}_{2}}^{2}+1}$,
∴C($\frac{2{k}_{2}}{{{k}_{2}}^{2}+1}$,$\frac{{{k}_{2}}^{2}-1}{{{k}_{2}}^{2}+1}$),
∵k2=4k1,∴C($\frac{8{k}_{1}}{16{{k}_{1}}^{2}+1}$,$\frac{16{{k}_{1}}^{2}-1}{16{{k}_{1}}^{2}+1}$),
∴直线BC的斜率kBC=-$\frac{1}{4{k}_{1}}$,
∴直线BC的方程为:y-$\frac{4{{k}_{1}}^{2}-1}{1+4{{k}_{1}}^{2}}$=-$\frac{1}{4{k}_{1}}$(x-$\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$),
即y=-$\frac{1}{4{k}_{1}}$x+1,
∴直线BC过定点(0,1).
②∵$\overrightarrow{BC}$=($\frac{8{k}_{1}}{16{{k}_{1}}^{2}+1}$-$\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$,$\frac{16{{k}_{1}}^{2}-1}{16{{k}_{1}}^{2}+1}$-$\frac{4{{k}_{1}}^{2}-1}{1+4{{k}_{1}}^{2}}$),
$\overrightarrow{BE}$=(-$\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$,1-$\frac{4{{k}_{1}}^{2}-1}{1+4{{k}_{1}}^{2}}$)=(-$\frac{8{k}_{1}}{1+4{{k}_{1}}^{2}}$,$\frac{2}{1+4{k}_{1}^{2}}$),
∴|$\overrightarrow{BC}$|•|$\overrightarrow{BE}$|=|$\overrightarrow{BC}$•$\overrightarrow{BE}$|=|$\frac{-64{k}_{1}^{2}}{(1+4{k}_{1}^{2})(1+16{k}_{1}^{2})}$+$\frac{64{k}_{1}^{2}}{(1+4{k}_{1}^{2})^{2}}$+$\frac{32{k}_{1}^{2}-2}{(1+4{k}_{1}^{2})•(1+16{k}_{1}^{2})}$-$\frac{2{k}_{1}^{2}-2}{(1+4{k}_{1}^{2})^{2}}$|
=|-$\frac{2+8{k}_{1}^{2}}{(1+4{k}_{1}^{2})^{2}}$+$\frac{62{k}_{1}^{2}+2}{(1+4{k}_{1}^{2})^{2}}$|
=$\frac{54{k}_{1}^{2}}{1+8{k}_{1}^{2}+16{k}_{1}^{4}}$,
=$\frac{54}{\frac{1}{{k}_{1}^{2}}+16{k}_{1}^{2}+8}$≤$\frac{54}{8+8}$=$\frac{27}{8}$,当k1=±2时取等号
故|$\overrightarrow{BC}$|•|$\overrightarrow{BE}$|的最大值$\frac{27}{8}$
点评 本题考查曲线轨迹方程的求解,考查直线恒过定点,以及向量的数量积运算和基本不等式,解题的关键是确定点B、C的坐标,求出直线BC的方程是,属于难题.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-2,\left.{-\frac{1}{3}}]$ | B. | $(-2,\left.{\frac{1}{2}}]$ | C. | $(-\frac{1}{3},\left.{\frac{1}{2}}]$ | D. | $(-1,\left.{\frac{1}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是三段论推理,但大前提错 | B. | 是三段论推理,但小前提错 | ||
| C. | 不是三段论推理,但结论正确 | D. | 不是三段论推理,且结论不正确 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com