
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(I)若曲线![]() ,参数方程为:
,参数方程为:![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程
的普通方程
(Ⅱ)若曲线![]() ,参数方程为
,参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() ,与曲线
,与曲线![]() 交点分别为
交点分别为![]() ,求
,求![]() 的取值范围,
的取值范围,
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点,PA=AD.
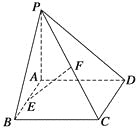
求证:(1)CD⊥PD;(2)EF⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于相关系数![]() 的说法不正确的是( )
的说法不正确的是( )
A. 相关系数![]() 越大两个变量间相关性越强;
越大两个变量间相关性越强;
B. 相关系数![]() 的取值范围为
的取值范围为![]() ;
;
C. 相关系数![]() 时两个变量正相关,
时两个变量正相关,![]() 时两个变量负相关;
时两个变量负相关;
D. 相关系数![]() 时,样本点在同一直线上。
时,样本点在同一直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两队学生参加“知识联想”抢答赛,比赛规则:①主持人依次给出两次提示,第一次提示后答对得2分,第二次提示后答对得1分,没抢到或答错者不得分;②主持人给出第一个提示后开始抢答,第一轮抢答出错失去第二轮答题资格;③每局比赛分两轮,若第一轮抢答者给出正确答案,则此局比赛结束,若第一轮答题者答错,主持人提示后另一队直接答题。如果甲、乙两队抢到答题权机会均等,并且势均力敌,第一个提示后答对概率均为![]() ;第二个提示后答对概率均为
;第二个提示后答对概率均为![]() ,
,![]() 为甲队在一局比赛中的分.
为甲队在一局比赛中的分.
(1)求甲在一局比赛中得分的分布列;
(2)若比赛共4局,求甲4局比赛中至少得6分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对“2019年3月在北京召开的第十三届全国人民代表大会第二次会议和政协第十三届全国委员会第二次会议”的关注度,某部门从年龄在15岁到65岁的人群中随机调查了100人,并得到如图所示的年龄频率分布直方图,在这100人中关注度非常髙的人数与年龄的统计结果如右表所示:

年龄 | 关注度非常高的人数 |
| 15 |
| 5 |
| 15 |
| 23 |
| 17 |
(Ⅰ)由频率分布直方图,估计这100人年龄的中位数和平均数;
(Ⅱ)根据以上统计数据填写下面的![]() 列联表,据此表,能否在犯错误的概率不超过
列联表,据此表,能否在犯错误的概率不超过![]() 的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
的前提下,认为以45岁为分界点的不同人群对“两会”的关注度存在差异?
(Ⅲ)按照分层抽样的方法从年龄在35岁以下的人中任选六人,再从六人中随机选两人,求两人中恰有一人年龄在25岁以下的概率是多少.
45岁以下 | 45岁以上 | 总计 | |
非常髙 | |||
一般 | |||
总计 |
参考数据:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为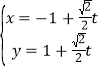 (
(![]() 为参数),圆
为参数),圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(Ⅰ)求直线![]() 及圆
及圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com