
【题目】已知函数![]() .
.
(1)求![]() 在区间
在区间![]() 上的值域;
上的值域;
(2)若过点![]() 存在
存在![]() 条直线与曲线
条直线与曲线![]() 相切,求
相切,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ; (2)
; (2) ![]() .
.
【解析】
(1)利用导数求得极值点比较f(-2)![]() ,
,![]() ,f(1)的大小即得结论;
,f(1)的大小即得结论;
(2)利用导数的几何意义得出切线方程4![]() ,设g(x)=4x3-6x2+t+3,则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,
,设g(x)=4x3-6x2+t+3,则“过点P(1,t)存在3条直线与曲线y=f(x)相切”,
等价于“g(x)有3个不同的零点”.利用导数判断函数的单调性进而得出函数的零点情况,得出结论;
(1)由![]() 得
得![]() .
.
令![]() ,得
,得![]() 或
或![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .
.
(2)设过点![]() 的直线与曲线
的直线与曲线![]() 相切于点
相切于点![]() ,
,
则![]() ,且切线斜率为
,且切线斜率为![]() ,
,
所以切线方程为![]() ,
,
因此![]() .
.
整理得![]() .
.
设![]() ,
,
则“过点![]() 存在3条直线与曲线
存在3条直线与曲线![]() 相切”等价于“
相切”等价于“![]() 有3个不同零点”.
有3个不同零点”.
![]() .
.
![]() 与
与![]() 的变化情况如下:
的变化情况如下:
|
| 0 |
| 1 |
|
|
| 0 |
| 0 |
|
|
|
|
|
|
|
所以, ![]() 是
是![]() 的极大值,
的极大值, ![]() 是
是![]() 的极小值.
的极小值.
当![]() ,即
,即![]() 时,
时,
此时![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,
上分别至多有1个零点,
所以![]() 至多有2个零点.
至多有2个零点.
当![]() ,即
,即![]() 时,
时,
此时![]() 在区间
在区间![]() 和
和![]() 上分别至多有1个零点,所以
上分别至多有1个零点,所以![]() 至多有
至多有![]() 个零点.
个零点.
当![]() 且
且![]() ,即
,即![]() 时,
时,
因为![]() ,
,![]() ,
,
所以![]() 分别在区间
分别在区间![]() ,
,![]() 和
和![]() 上恰有1个零点.
上恰有1个零点.
由于![]() 在区间
在区间![]() 和
和![]() 上单调,
上单调,
所以![]() 分别在区间
分别在区间![]() 和
和![]() 上恰有1个零点.
上恰有1个零点.
综上可知,当过点![]() 存在
存在![]() 条直线与曲线
条直线与曲线![]() 相切时,
相切时,![]() 的取值范围是
的取值范围是![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】已知向量![]() = (1,2sinθ),
= (1,2sinθ),![]() = (sin(θ+
= (sin(θ+![]() ),1),θ
),1),θ![]() R。
R。
(1) 若![]() ⊥
⊥![]() ,求 tanθ的值;
,求 tanθ的值;
(2) 若![]() ∥
∥![]() ,且 θ
,且 θ![]() (0,
(0,![]() ),求 θ的值
),求 θ的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解高三复习效果,从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩,分成6组制成频率分布直方图如图所示:
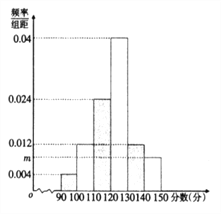
(1)求![]() 的值及这50名同学数学成绩的平均数
的值及这50名同学数学成绩的平均数![]() ;
;
(2)该学校为制定下阶段的复习计划,从成绩在![]() 的同学中选出3位作为代表进行座谈,若已知成在
的同学中选出3位作为代表进行座谈,若已知成在![]() 的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
的同学中男女比例为2:1,求至少有一名女生参加座谈的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B,C,D是空间不共面的四点,它们到平面a的距离之比依次为1:1:1:2,则满足条件的平面a的个数是:
A. 1 B. 4 C. 7 D. 8.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间D上的函数![]() ,若存在正整数k,使不等式
,若存在正整数k,使不等式![]() 恒成立,则称
恒成立,则称![]() 为
为![]() 型函数.
型函数.
(1)设函数![]() ,定义域
,定义域![]() .若
.若![]() 是
是![]() 型函数,求实数a的取值范围;
型函数,求实数a的取值范围;
(2)设函数![]() ,定义域
,定义域![]() .判断
.判断![]() 是否为
是否为![]() 型函数,并给出证明.
型函数,并给出证明.
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某台函数计算器上有一个显示屏和两个操作键.若按一下第一个操作键,则将原显示屏上的数变为![]() (
(![]() 表示不超过实数x的最大整数);若按一下第二个操作键,则将原显示屏上的数变为
表示不超过实数x的最大整数);若按一下第二个操作键,则将原显示屏上的数变为![]() .称按一下任意一个操作键为一次操作.现在显示屏上的数为1.问:
.称按一下任意一个操作键为一次操作.现在显示屏上的数为1.问:
(1)是否可以经过有限次操作,显示屏上出现整数2000?说明理由.
(2)小于2000的整数中有多少个数可以经过有限次操作在显示屏上出现?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三边长分别为a,b,c,其面积为S,则
的三边长分别为a,b,c,其面积为S,则![]() 的内切圆O的半径
的内切圆O的半径![]() .这是一道平面几何题,其证明方法采用“等面积法”设空间四面体
.这是一道平面几何题,其证明方法采用“等面积法”设空间四面体![]() 四个面的面积分别为积为V,内切球半径为R.请用类比推理方法猜测对空间四面体
四个面的面积分别为积为V,内切球半径为R.请用类比推理方法猜测对空间四面体![]() 存在类似结论为______.
存在类似结论为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海滨浴场一天的海浪高度![]() 是时间
是时间![]() 的函数,记作
的函数,记作![]() ,下表是某天各时的浪高数据:
,下表是某天各时的浪高数据:
| 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 0.99 | 1.5 |
(1)选用一个三角函数来近似描述这个海滨浴场的海浪高度![]() 与时间
与时间![]() 的函数关系;
的函数关系;
(2)依据规定,当海浪高度不少于![]() 时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的
时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的![]() 至
至![]() 之间,有多少时间可供冲浪爱好者进行冲浪?
之间,有多少时间可供冲浪爱好者进行冲浪?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com