
����Ŀ��ij��λ�����֯��һ�ν���������Ϊ��ɽ�����Ӿ�飬��ÿ��ְ������μ�����һ�飮�ڲμӻ��ְ���У�������ռ42. 5%��������ռ47. 5%��������ռ10%. ��ɽ���ְ��ռ�μӻ�������� ![]() ���Ҹ����У�������ռ50%��������ռ40%��������ռ10%. Ϊ���˽���鲻ͬ�����ε�ְ���Ա��λ������̶ȣ����÷ֲ���������Ӳμӻ��ȫ��ְ���г�ȡһ������Ϊ200����������ȷ����
���Ҹ����У�������ռ50%��������ռ40%��������ռ10%. Ϊ���˽���鲻ͬ�����ε�ְ���Ա��λ������̶ȣ����÷ֲ���������Ӳμӻ��ȫ��ְ���г�ȡһ������Ϊ200����������ȷ����
��1����Ӿ���У������ˡ������ˡ������˷ֱ���ռ�ı�����
��2����Ӿ���У������ˡ������ˡ������˷ֱ�Ӧ��ȡ��������
���𰸡�
��1���⣺���ɽ������Ϊx����Ӿ���У������ˡ������ˡ���������ռ�����ֱ�Ϊa��b��c��
���� ![]()
���b��50%��c��10%��
��a��100%��50%��10%��40%��
����Ӿ���У������ˡ������ˡ���������ռ�����ֱ�Ϊ40%��50%��10%
��2���⣺�ɣ�1��֪��Ӿ���У������ˡ������ˡ���������ռ�����ֱ�Ϊ40%��50%��10%��
���ȡ������������Ϊ200�� ![]() ��40%��60(��)��
��40%��60(��)��
��ȡ������������Ϊ200�� ![]() ��50%��75(��)��
��50%��75(��)��
��ȡ������������Ϊ200�� ![]() ��10%��15(��)��
��10%��15(��)��
����Ӿ���У������ˡ������ˡ������˷ֱ�Ӧ��ȡ������Ϊ60�ˣ�75�ˣ�15��
��������(1)��������������ɽ������������Ϊ��Ӿ���У������ˡ������ˡ���������ռ�����ֱ�Ϊa��b��c����ͨ���г����̿��������Ӧ��ֵ��
��2���ɣ�1������������ˡ������ˡ������˸�ռ�����������˱��������ȡ��������


 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l1����A(0,1)��l2����B(5,0)�����l1��l2��l1��l2�ľ���Ϊ5����l1 �� l2�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=|ax��4|��|ax+8|��a��R
����a=2ʱ���ⲻ��ʽf��x����2��
������f��x����k���������k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��= ![]() x3��ax2+��a2��1��x+b��a��b��R������ͼ���ڵ㣨1��f��1�����������߷���Ϊx+y��3=0��
x3��ax2+��a2��1��x+b��a��b��R������ͼ���ڵ㣨1��f��1�����������߷���Ϊx+y��3=0��
��1����a��b��ֵ��
��2������f��x���ĵ������䣬�����f��x��������[��2��4]�ϵ����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ABCD�У�AB��AD��AD��BC��AB=BC=2AD=2��E��F�ֱ�ΪBC��CD���е㣬��AΪԲ�ģ�ADΪ�뾶��Բ��AB��G����P�� ![]() ���˶�����ͼ������
���˶�����ͼ������ ![]() =��
=�� ![]() +��
+�� ![]() �����Цˣ��̡�R����6��+�̵�ȡֵ��Χ�ǣ� ��
�����Цˣ��̡�R����6��+�̵�ȡֵ��Χ�ǣ� �� 
A.[1�� ![]() ]
]
B.[ ![]() ��2
��2 ![]() ]
]
C.[2��2 ![]() ]
]
D.[1��2 ![]() ]
]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=|x��1|+|x+1|��
��1����f��x����x+2�Ľ⼯��
��2��������x��Rʹ����ʽ ![]() ��������ʵ��a��ȡֵ��Χ��
��������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������� ![]() �У�ƽ��PAD��ABCD��AB=AD����BAD=60�㣬E��F�ֱ���AP��AD���е�.
�У�ƽ��PAD��ABCD��AB=AD����BAD=60�㣬E��F�ֱ���AP��AD���е�.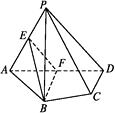
��֤��
��1��ֱ��EF��ƽ��PCD��
��2��ƽ��BEF��ƽ��PAD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫���߷���Ϊ16x2��9y2=144��
��1�����˫���ߵ�ʵ�᳤�����᳤�������ʣ�
��2����������C�Ķ����Ǹ�˫���ߵ����ģ������������㣬��������C�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC����ƽ������һ��P��D��E�ֱ���PB��AB�ϵĵ㣬��D��E��ƽ��ƽ����BC���Ի������ƽ������������Ľ��ߣ���˵������������.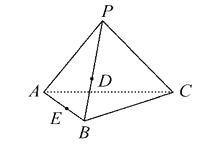
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com