
【题目】已知椭圆 ![]() 的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形.
的左、右焦点分别为F1、F2 , 短轴两个端点为A、B,且四边形F1AF2B是边长为2的正方形. 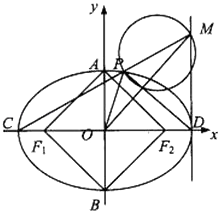
(1)求椭圆的方程;
(2)若C、D分别是椭圆长的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P.证明: ![]() 为定值.
为定值.
(3)在(2)的条件下,试问x轴上是否存异于点C的定点Q,使得以MP为直径的圆恒过直线DP、MQ的交点,若存在,求出点Q的坐标;若不存在,请说明理由.
【答案】
(1)解:a=2,b=c,a2=b2+c2,∴b2=2;
∴椭圆方程为 ![]()
(2)解:C(﹣2,0),D(2,0),设M(2,y0),P(x1,y1),
则 ![]()
直线CM: ![]() ,代入椭圆方程x2+2y2=4,
,代入椭圆方程x2+2y2=4,
得 ![]()
∵x1=﹣ ![]()
![]() ,∴
,∴ ![]() ,∴
,∴ ![]() ,∴
,∴ ![]()
∴ ![]() (定值)
(定值)
(3)解:设存在Q(m,0)满足条件,则MQ⊥DP
![]()
则由 ![]() ,从而得m=0
,从而得m=0
∴存在Q(0,0)满足条件
【解析】(1)由题意知a=2,b=c,b2=2,由此可知椭圆方程为 ![]() .(2)设M(2,y0),P(x1 , y1),则
.(2)设M(2,y0),P(x1 , y1),则 ![]() ,直线CM:
,直线CM: ![]() ,代入椭圆方程x2+2y2=4,得
,代入椭圆方程x2+2y2=4,得 ![]() ,然后利用根与系数的关系能够推导出
,然后利用根与系数的关系能够推导出 ![]() 为定值.(3)设存在Q(m,0)满足条件,则MQ⊥DP.
为定值.(3)设存在Q(m,0)满足条件,则MQ⊥DP. ![]() ,再由
,再由 ![]() ,由此可知存在Q(0,0)满足条件.
,由此可知存在Q(0,0)满足条件.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,下列条件:
①∠B+∠DAC=90°,
②∠B=∠DAC,
③![]() ,
,
④AB2=BD·BC.
其中一定能够判定△ABC是直角三角形的共有( )
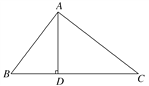
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一位网民在网上光顾某网店,经过一番浏览后,对该店铺中的A,B,C三种商品有购买意向.已知该网民购买A种商品的概率为 ![]() ,购买B种商品的槪率为
,购买B种商品的槪率为 ![]() ,购买C种商品的概率为
,购买C种商品的概率为 ![]() .假设该网民是否购买这三种商品相互独立
.假设该网民是否购买这三种商品相互独立
(1)求该网民至少购买2种商品的概率;
(2)用随机变量η表示该网民购买商品的种数,求η的槪率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
, ![]() 分别是椭圆
分别是椭圆![]() :
: ![]() (
(![]() )的左、右焦点,离心率为
)的左、右焦点,离心率为![]() ,
, ![]() ,
, ![]() 分别是椭圆的上、下顶点,
分别是椭圆的上、下顶点, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 作直线
作直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,求三角形
两点,求三角形![]() 面积的最大值(
面积的最大值(![]() 是坐标原点).
是坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
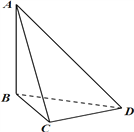
【题目】刘徽(约公元 225 年—295 年)是魏晋时期伟大的数学家,中国古典数学理论的奠基人之一,他的杰作《九章算术注》和《海岛算经》是中国宝贵的古代数学遗产. 《九章算术·商功》中有这样一段话:“斜解立方,得两壍堵. 斜解壍堵,其一为阳马,一为鳖臑.” 刘徽注:“此术臑者,背节也,或曰半阳马,其形有似鳖肘,故以名云.” 其实这里所谓的“鳖臑(biē nào)”,就是在对长方体进行分割时所产生的四个面都为直角三角形的三棱锥. 如图,在三棱锥![]() 中,
中, ![]() 垂直于平面
垂直于平面![]() ,
, ![]() 垂直于
垂直于![]() ,且
,且 ![]() ,则三棱锥
,则三棱锥![]() 的外接球的球面面积为__________.
的外接球的球面面积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近几年,电商行业的蓬勃发展也带动了快递业的高速发展.某快递配送站每天至少要完成1800件包裹的配送任务,该配送站有8名新手快递员和4名老快递员,但每天最多安排10人进行配送.已知每个新手快递员每天可配送240件包裹,日工资320元;每个老快递员每天可配送300件包裹,日工资520元.
(1)求该配送站每天需支付快递员的总工资最小值;
(2)该配送站规定:新手快递员某个月被评为“优秀”,则其下个月的日工资比这个月提高12%.那么新手快递员至少连续几个月被评为“优秀”,日工资会超过老快递员?
(参考数据: ![]() ,
, ![]() ,
, ![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com