
【题目】对于函数f(x),若存在x0∈R,使得f(x0)=x0成立,则称x0为f(x)的天宫一号点.已知函数f(x)=ax2+(b-7)x+18的两个天宫一号点分别是-3和2.
(1)求a,b的值及f(x)的表达式;
(2)当函数f(x)的定义域是[t,t+1]时,求函数f(x)的最大值g(t).
 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大.
有关系”的可信度越大.
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() 的值分别是
的值分别是![]() 和0.3.
和0.3.
③根据具有线性相关关系的两个变量的统计数据所得的回归直线方程为![]() 中,
中, ![]() ,
,
则![]() .正确的个数是( )
.正确的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数对![]() 一切实数
一切实数![]() 都有
都有![]() ,且当
,且当![]() 时,
时,![]() ,又
,又![]() .
.
(1)判断该函数的奇偶性并说明理由;、
(2)试判断该函数在![]() 上的单调性;
上的单调性;
(3)求![]() 在区间
在区间![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
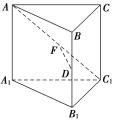
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形![]() 是边长为4的正方形,点
是边长为4的正方形,点![]() 为
为![]() 边上任意一点(与点
边上任意一点(与点![]() 不重合),连接
不重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,设
,设![]() .
.
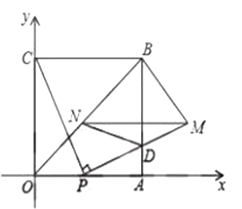
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示)
的代数式表示)
(2)试判断线段![]() 的长度是否随点
的长度是否随点![]() 的位置的变化而改变?并说明理由.
的位置的变化而改变?并说明理由.
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 的面积最小.
的面积最小.
(4)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用含
的坐标(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区预计从2015年初开始的第![]() 月,商品
月,商品![]() 的价格
的价格![]() (
(![]() ,
, ![]() ,价格单位:元),且第
,价格单位:元),且第![]() 月该商品的销售量
月该商品的销售量![]() (单位:万件).
(单位:万件).
(1)商品![]() 在2015年的最低价格是多少?
在2015年的最低价格是多少?
(2)2015年的哪一个月的销售收入最少,最少是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高三年级有3名男生和1名女生为了报某所大学,事先进行了多方详细咨询,并根据自己的高考成绩情况,最终估计这3名男生报此所大学的概率都是![]() ,这1名女生报此所大学的概率是
,这1名女生报此所大学的概率是![]() .且这4人报此所大学互不影响。
.且这4人报此所大学互不影响。
(Ⅰ)求上述4名学生中报这所大学的人数中男生和女生人数相等的概率;
(Ⅱ)在报考某所大学的上述4名学生中,记![]() 为报这所大学的男生和女生人数的和,试求
为报这所大学的男生和女生人数的和,试求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com