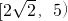
分析:先根据约束条件画出可行域,设z=

,再利用z的几何意义求最值,再利用几何意义求最值,只需求出可行域内的点到原点距离的最值,从而得到z最值即可.
解答:
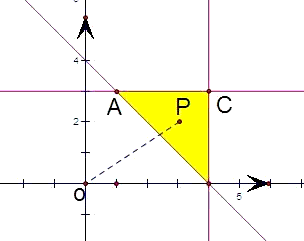
解:先根据约束条件画出可行域,
z=

,
表示可行域内点到原点距离,
当在点C时,z最大,最大值为5,
当z是点O到直线:x+y-4=0的距离时,z最小,最小值为
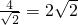
,
故答案为:
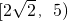
.
点评:本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.

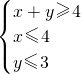 ,则
,则 的取值范围是 ________.
的取值范围是 ________.