
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象
在某一个周期内的图象
时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解
的解
析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]()
![]() 个单位长度,得到
个单位长度,得到![]() 的图
的图
象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】圆锥![]() 如图①所示,图②是它的正(主)视图.已知圆
如图①所示,图②是它的正(主)视图.已知圆![]() 的直径为
的直径为![]() ,
, ![]() 是圆周上异于
是圆周上异于![]() 的一点,
的一点, ![]() 为
为![]() 的中点.
的中点.
(I)求该圆锥的侧面积S;
(II)求证:平面![]() ⊥平面
⊥平面![]() ;
;
(III)若∠CAB=60°,在三棱锥![]() 中,求点
中,求点![]() 到平面
到平面![]() 的距离.
的距离.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2-lnx。
(Ⅰ)当a=![]() 时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
时,判断f(x)的单调性;(Ⅱ)设f(x)≤x3+4x-lnx,在定义域内恒成立,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变.假设在放射性同位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M0 ![]() ,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是﹣10In2(太贝克/年),则M(60)=( )
A.5太贝克
B.75In2太贝克
C.150In2太贝克
D.150太贝克
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax3+bx2+cx的极小值为﹣8,其导函数y=f′(x)的图象经过点 ![]() ,如图所示,
,如图所示, 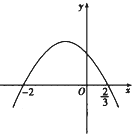
(1)求f(x)的解析式;
(2)若对x∈[﹣3,3]都有f(x)≥m2﹣14m恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+ ![]() (a∈R)g(x)=lnx.
(a∈R)g(x)=lnx.
(1)若对任意的实数a,函数f(x)与g(x)的图象在x=x0处的切线斜率总相等,求x0的值;
(2)若a>0,对任意x>0,不等式f(x)﹣g(x)≥1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,对任意的实数x,y都有f(x+y)=f(x)+f(y)+ ![]() ,且f(
,且f( ![]() )=0,当x>
)=0,当x> ![]() 时,f(x)>0.
时,f(x)>0.
(1)求f(1);
(2)判断函数f(x)的单调性,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com