【题目】《宋人扑枣图轴》是作于宋朝的中国古画，现收藏于中国台北故宫博物院.该作品简介：院角的枣树结实累累，小孩群来攀扯，枝桠不停晃动，粒粒枣子摇落满地，有的牵起衣角，有的捧着盘子拾取，又玩又吃，一片兴高采烈之情，跃然于绢素之上.甲、乙、丙、丁四人想根据该图编排一个舞蹈，舞蹈中他们要模仿该图中小孩扑枣的爬、扶、捡、顶四个动作，四人每人模仿一个动作.若他们采用抽签的方式来决定谁模仿哪个动作，则甲不模仿“爬”且乙不模仿“扶”的概率是（ ）
A.
B.
C.
D.
科目：高中数学 来源： 题型：
【题目】某校开设了素描摄影剪纸书法四门选修课，要求每位同学都要选择其中的两门课程.已知甲同学选了素描，乙与甲没有相同的课程，丙与甲恰有一门课程相同，丁与丙没有相同课程.则以下说法错误的是（ ）
A.丙有可能没有选素描B.丁有可能没有选素描
C.乙丁可能两门课都相同D.这四个人里恰有2个人选素描
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；
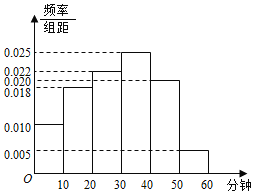
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”，已知“体育迷”中有10名女性.
非体育迷 | 体育迷 | 合计 | |
男 | |||
女 | |||
合计 |
（1）根据已知条件完成下面的
列联表，并据此资料你是否认为“体育迷”与性别有关？
（2）将日均收看该体育项目不低于50分钟的观众称为“超级体育迷”，已知“超级体育迷”中有2名女性，若从“超级体育迷”中任意选取2人，求至少有1名女性观众的概率.
附：参考公式：
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在
中，
，
，AB的垂直平分线分别交AB，AC于D、E（图一），沿DE将
折起，使得平面
平面BDEC（图二）．
（1）若F是AB的中点，求证：
平面ADE．
（2）P是AC上任意一点，求证：平面
平面PBE．
（3）P是AC上一点，且
平面PBE，求二面角
的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
：
（
）的左、右焦点分别为
、
，过右焦点的直线
：
与椭圆交于
，
两点.当
时，是椭圆的下顶点，且
的周长为6.
（1）求椭圆的方程；
（2）设椭圆的右顶点为
，直线
、
分别与直线
交于
、
点，证明：当
变化时，以线段
为直径的圆与直线相切.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
是椭圆
的左、右焦点，离心率为
，
是平面内两点，满足
，线段
的中点
在椭圆上，
周长为12.
（1）求椭圆
的方程；
（2）若过
的直线
与椭圆交于
，求
（其中
为坐标原点)的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】据统计，仅在北京地区每天就有500万单快递等待派送，近5万多名快递员奔跑在一线，快递网点人员流动性也较强，各快递公司需要经常招聘快递员，保证业务的正常开展.下面是50天内甲、乙两家快递公司的快递员的每天送货单数统计表：
送货单数 | 30 | 40 | 50 | 60 | |
天数 | 甲 | 10 | 10 | 20 | 10 |
乙 | 5 | 15 | 25 | 5 | |
已知这两家快递公司的快递员的日工资方案分别为：甲公司规定底薪
元，每单抽成
元；乙公司规定底薪
元，每日前
单无抽成，超过单的部分每单抽成
元．
（1）分别求甲、乙快递公司的快递员的日工资
（单位：元）与送货单数
的函数关系式；
（2）若将频率视为概率，回答下列问题：
①记甲快递公司的快递员的日工资为
（单位：元），求的分布列和数学期望；
②小赵拟到甲、乙两家快递公司中的一家应聘快递员的工作，如果仅从日收入的角度考虑，请你利用所学的统计学知识为他作出选择，并说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）＝xlnx﹣x+1，g（x）＝ex﹣ax，a∈R．
（Ⅰ）求f（x）的最小值；
（Ⅱ）若g（x）≥1在R上恒成立，求a的值；
（Ⅲ）求证：
．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
