
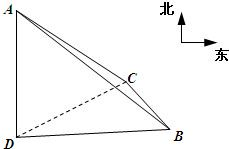
 为测量某塔的高度,同学甲先在观察点C测得塔顶A在南偏西80°方向上,仰角为45°,然后沿南偏东40°方向前进30米到B点后,测得塔顶A仰角为30°,试根据同学甲测得的数据计算此塔AD的高度.(其中点A为塔顶,点D为塔顶A在地面上的射影,点B、C、D均在地面上,不考虑同学甲的身高)
为测量某塔的高度,同学甲先在观察点C测得塔顶A在南偏西80°方向上,仰角为45°,然后沿南偏东40°方向前进30米到B点后,测得塔顶A仰角为30°,试根据同学甲测得的数据计算此塔AD的高度.(其中点A为塔顶,点D为塔顶A在地面上的射影,点B、C、D均在地面上,不考虑同学甲的身高)  名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
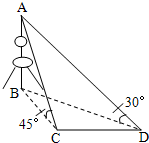 如图所示,要测量底部不能到达的某电视塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°,在水平面上测得∠BCD=120°,C、D两地相距500m,则电视塔AB的高度是( )
如图所示,要测量底部不能到达的某电视塔AB的高度,在塔的同一侧选择C、D两观测点,且在C、D两点测得塔顶的仰角分别为45°、30°,在水平面上测得∠BCD=120°,C、D两地相距500m,则电视塔AB的高度是( )A、100
| ||
| B、400m | ||
C、200
| ||
| D、500m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com