
(本题14分)有两个不透明的箱子,每个箱子都装有![]() 个完全相同的小球,球上分别标有数字
个完全相同的小球,球上分别标有数字![]() 。
。
甲从其中一个箱子中摸出一个球,乙从另一个箱子摸出一个球,谁摸出的球上标的数字大谁就获胜(若数字相同则为平局),求甲获胜的概率;
摸球方法与(1)同,若规定:两人摸到的球上所标数字相同甲获胜,所标数字不相同则乙获胜,这样规定公平吗?请说明理由。
科目:高中数学 来源:2011年福建省罗源县第一中学高一上学期期中考试数学 题型:解答题
((本题14分)定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数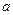 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年福建省龙岩市高三上学期期末考试数学理卷(普通学校) 题型:解答题
.(本题满分14分)
设函数 =
=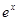 (
( 为自然对数的底数),
为自然对数的底数), ,记
,记 .
.
(Ⅰ)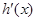 为
为 的导函数,判断函数
的导函数,判断函数 的单调性,并加以证明;
的单调性,并加以证明;
(Ⅱ)若函数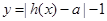 =0有两个零点,求实数
=0有两个零点,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高二10月月考数学理卷 题型:解答题
(本题满分14分)已知函数 (
(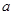 是常数)
是常数)
(I) 求函数 的单调区间;
的单调区间;
(II) 当 在
在 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数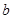 的取值范围;
的取值范围;
(III) 求证:当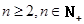 时
时 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省高二10月月考数学理卷 题型:解答题
(本题满分14分)已知函数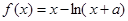 (
( 是常数)
是常数)
(I) 求函数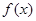 的单调区间;
的单调区间;
(II) 当 在
在 处取得极值时,若关于x的方程
处取得极值时,若关于x的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数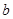 的取值范围;
的取值范围;
(III) 求证:当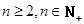 时
时 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com