
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的已套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
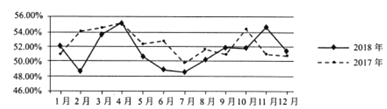
A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 这两年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
【题目】如图,多面体 ABCDEF中,四边形ABCD是边长为2的菱形,且平面ABCD⊥平面DCE.AF∥DE,且AF=![]() DE=2,BF=2
DE=2,BF=2![]() .
.
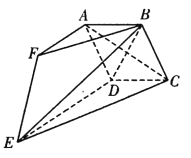
(1)求证:AC⊥BE;
(2)若点F到平面DCE的距离为![]() ,求直线EC与平面BDE所成角的正弦值.
,求直线EC与平面BDE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:x2=2py(p>0)的焦点到直线l:2x﹣y﹣1=0的距离为![]() .
.
(1)求抛物线的方程;
(2)过点P(0,t)(t>0)的直线l与抛物线C交于A,B两点,交x轴于点Q,若抛物线C上总存在点M(异于原点O),使得∠PMQ=∠AMB=90°,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次函数f(x)=ax2﹣2bx+8.
(1)设集合P={1,2,3}和Q={2,3,4,5},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
(2)设集合P=[1,3]和Q[2,5],分别从集合P和Q中随机取一个实数作为a和b,求函数y=f(x)在区间(﹣∞,2]上有零点且为减函数的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据气象局统计,某市2019年从1月1日至1月30日这30天里有26天出现雾霾天气.国际上通常用环境空气质量指数(AQI)来描述污染状况,下表是某气象观测点记录的连续4天里,该市AQI指数![]() 与当天的空气水平可见度
与当天的空气水平可见度![]() 的情况.
的情况.
AQI指数 | 900 | 700 | 300 | 100 |
空气水平可见度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)设![]() ,根据表中的数据,求出
,根据表中的数据,求出![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)若某天该市AQT指数![]() ,那么当天空气水平可见度大约为多少?
,那么当天空气水平可见度大约为多少?
附:参考数据:![]() ,
,![]() .
.
参考公式:线性回归力程![]() 中,
中,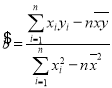 ,
,![]() ,其中
,其中![]() 为样本平均数.
为样本平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() (1+cos2θ)=8sinθ.
(1+cos2θ)=8sinθ.
(1)求曲线C的普通方程;
(2)直线l的参数方程为![]() ,t为参数直线
,t为参数直线![]() 与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线
与y轴交于点F与曲线C的交点为A,B,当|FA||FB|取最小值时,求直线![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种棉花中各抽测了25根棉花的纤维长度(单位: ![]() ) 组成一个样本,且将纤维长度超过315
) 组成一个样本,且将纤维长度超过315![]() 的棉花定为一级棉花.设计了如下茎叶图:
的棉花定为一级棉花.设计了如下茎叶图:

(1)根据以上茎叶图,对甲、乙两种棉花的纤维长度作比较,写出两个统计结论(不必计算);
(2)从样本中随机抽取甲、乙两种棉花各2根,求其中恰有3根一级棉花的概率;
(3)用样本估计总体,将样本频率视为概率,现从甲、乙两种棉花中各随机抽取1根,求其中一级棉花根数X的分布列及数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.下图所示的阳马![]() 中,侧棱
中,侧棱![]() 底面ABCD,且
底面ABCD,且![]() ,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体
,则当点E在下列四个位置:PA中点、PB中点、PC中点、PD中点时分别形成的四面体![]() 中,鳖臑有( )个.
中,鳖臑有( )个.
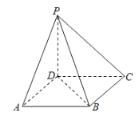
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com