练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    20．若一个几何体的三视图如图所示，则该几何体的表面积为3$\sqrt{3}$+6．

    分析 通过三视图判断几何体的形状，利用三视图的数据和正六边形的特征，求出几何体的表面积即可．

    解答 解：由三视图可知，几何体是正六棱柱：底面是边长为1和的正六边形，几何体的高为1，
    则几何体的表面积为：S=2×$\frac{1}{2}×{1}^{2}×\frac{\sqrt{3}}{2}$×6+6×1×1=3$\sqrt{3}$+6，
    故答案为：3$\sqrt{3}$+6．

    点评 本题考查三视图与直观图的关系，几何体的表面积的求法，判断三视图复原几何体的形状是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

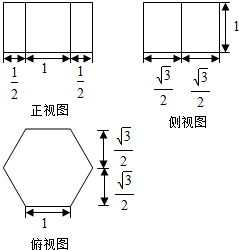
    科目：高中数学 来源： 题型：选择题

    10．在空间直角坐标系中，以A（m，1，9），B（10，-1，6），C（2，4，3）为顶点的三角形是等腰三角形，其中m∈Z，则m的值为（　　）
    A．-4B．4C．-6或4D．6或4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

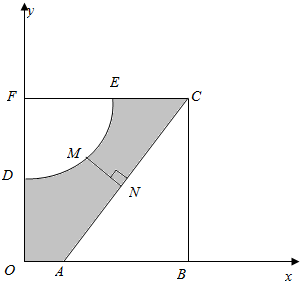    11．如图，河的两岸，分别有生活小区ABC和DEF，其中AB⊥BC，EF⊥DF，DF⊥AB，C，E，F三点共线，FD与BA的延长线交于点O，测得AB=3km，BC=4km，DF=$\frac{9}{4}$km，FE=3km，EC=$\frac{3}{2}$km．若以OA，OD所在直线为x，y轴建立平面直角坐标系xoy，则河岸DE可看成是曲线y=$\frac{x+b}{x+a}$（其中a，b为常数）的一部分，河岸AC可看成是直线y=kx+m（其中k，m为常数）的一部分．
    （1）求a，b，k，m的值；
    （2）现准备建一座桥MN，其中M，N分别在DE，AC上，且MN⊥AC，设点M的横坐标为t．
    ①请写出桥MN的长l关于t的函数关系式l=f（t），并注明定义域；
    ②当t为何值时，l取得最小值？最小值是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．如图，已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），离心率为$\frac{1}{2}$．过原点的直线与椭圆C交于A、B两点（A，B不是椭圆C的顶点），点D在椭圆C上，且AD⊥AB．
    （1）求椭圆C的右准线方程为：x=4．求椭圆C的方程；
    （2）设直线BD、AB的斜率分别为k1，k2，求$\frac{{k}_{1}}{{k}_{2}}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若直线过点（-1，1），（2，2），则此直线的斜率为（　　）
    A．3B．$\frac{1}{3}$C．-3D．-$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需要维修），其他三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：米），修建此矩形场地围墙的总费用为y（单位：元）．
    （1）将y表示为x的函数；
    （2）写出函数f（x）=y的单调区间，并证明；
    （3）根据（2），试确定x，试修建此矩形场地围墙的总费用最小，并求出最小总费用．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知cosθ=$\frac{5}{13}$，θ∈（π，2π），求sin（$θ-\frac{π}{6}$），cos（$θ-\frac{π}{6}$）及tan（$θ-\frac{π}{6}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知角α的终边在图中阴影表示的范围内（不包括边界），那么角α的集合是{α|k•180°+45°＜α＜k•180°+135°，k∈Z}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知函数f（x）=4x3-3x2cosθ+$\frac{3}{16}$cosθ其中x∈R，θ为参数，且0≤θ≤2π．
    （1）当cosθ=0时，判断函数f（x）是否有极值；
    （2）要使函数f（x）的极小值大于零，求参数θ的取值范围．

    查看答案和解析>>

    同步练习册答案