
【题目】已知![]() 的三个顶点
的三个顶点![]() ,
,![]() ,
,![]() ,其外接圆为
,其外接圆为![]() .对于线段
.对于线段![]() 上的任意一点
上的任意一点![]() ,
,
若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,则
的中点,则![]() 的半径
的半径![]() 的取值范围__________.
的取值范围__________.
科目:高中数学 来源: 题型:
【题目】已知在三角形ABC中,AB<AC,∠BAC=90°,边AB,AC的长分别为方程x2﹣2(1![]() )x+4
)x+4![]() 0的两个实数根,若斜边BC上有异于端点的E,F两点,且EF=1,则
0的两个实数根,若斜边BC上有异于端点的E,F两点,且EF=1,则![]() 的取值范围为_____.
的取值范围为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在国庆期间,某商场进行优惠大酬宾活动,在活动期间,商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额(![]() 元)后,还可按如下方案获得相应金额(
元)后,还可按如下方案获得相应金额(![]() 元)的奖券:
元)的奖券: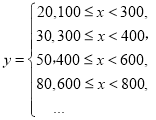 根据上述优惠方案,顾客在该商场购物可以获得双重优惠例如,购买标价为300元的商品,则消费金额为240元,获得的优惠额为:
根据上述优惠方案,顾客在该商场购物可以获得双重优惠例如,购买标价为300元的商品,则消费金额为240元,获得的优惠额为:![]() (元).设购买商品得到的
(元).设购买商品得到的![]() ,试问:
,试问:
(1)购买一件标价为800元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,要使顾客购买某商品获得30%的优惠率,则该商品的标价是多少?
(元)内的商品,要使顾客购买某商品获得30%的优惠率,则该商品的标价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() C的极坐标方程为
C的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 分别交
分别交![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第23届冬季奥运会于2018年2月9日至2月25日在韩国平昌举行,期间正值我市学校放寒假,寒假结束后,某校工会对全校教职工在冬季奥运会期间每天收看比赛转播的时间作了一次调查,得到如下频数分布表:

(1)若讲每天收看比赛转播时间不低于3小时的教职工定义为“体育达人”,否则定义为“非体育达人”,请根据频数分布表补全![]() 列联表:
列联表:

并判断能否有90%的把握认为该校教职工是否为“体育达人”与“性别”有关;
(2)在全校“体育达人”中按性别分层抽样抽取6名,再从这6名“体育达人”中选取2名作冬奥会知识讲座.记其中女职工的人数为![]() ,求的
,求的![]() 分布列与数学期望.
分布列与数学期望.
附表及公式:
![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.若
的左、右焦点.若![]() 是该椭圆上的一个动点,
是该椭圆上的一个动点,![]() 的最大值为1.
的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() (
(![]() 与
与![]() 不重合),则直线
不重合),则直线![]() 与
与![]() 轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调递增区间;
的单调递增区间;
(2)对于![]() ,
,![]() 为任意实数,关于
为任意实数,关于![]() 的方程
的方程![]() 恰好有两个不等实根,求实数
恰好有两个不等实根,求实数![]() 的值;
的值;
(3)在(2)的条件下,若不等式![]() 在
在![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com