
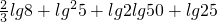 的值;
的值;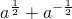 的值.
的值.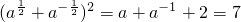 .
.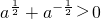 ,可得
,可得 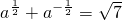 .…(14分)
.…(14分)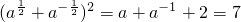 .再由
.再由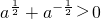 ,求得
,求得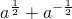 的值.
的值.

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013届浙江省杭州市萧山五校高二下期中理科数学试卷(解析版) 题型:解答题
数列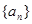 的前
的前 项和
项和 满足
满足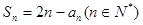 .
.
(1)计算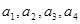 的值;
的值;
(2)猜想数列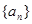 的通项公式并用数学归纳法证明.
的通项公式并用数学归纳法证明.
查看答案和解析>>
科目:高中数学 来源:2010福建省高二下学期期末考试理科数学卷 题型:解答题
甲、乙、丙三人轮流投掷一枚质地均匀的正方体骰子,规则如下:如果某人某一次掷出1点,则下一次继续由此人掷,如果掷出其他点数,则另外两个人抓阄决定由谁来投掷,且第一次由甲投掷。
设第n次由甲投掷的概率是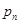 ,由乙或丙投掷的概率均为
,由乙或丙投掷的概率均为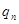 .
.
(1)计算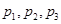 的值;
的值;
(2)求数列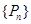 的通项公式;
的通项公式;
(3)如果一次投掷中,由任何两个人投掷的概率之差的绝对值小于0.001,则称此次投掷是“机会接近均等”,那么从第几次投掷开始,机会接近均等?
查看答案和解析>>
科目:高中数学 来源:2010年河北省高一下学期期末考试数学试题 题型:解答题
(本题满分12分)
已知数列 中
中 点
点
 在直线
在直线 上.
上.
(1)计算 的值;
的值;
(2)令 ,求证
,求证 是等比数列;
是等比数列;
(3)设 、
、 分别为数列
分别为数列 、
、 的前
的前 项和,是否存在实数
项和,是否存在实数 ,使得数列
,使得数列 为等差数列?若存在,试求出
为等差数列?若存在,试求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com