
【题目】某销售公司在当地![]() 、
、![]() 两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了
两家超市各有一个销售点,每日从同一家食品厂一次性购进一种食品,每件200元,统一零售价每件300元,两家超市之间调配食品不计费用,若进货不足食品厂以每件250元补货,若销售有剩余食品厂以每件150回收.现需决策每日购进食品数量,为此搜集并整理了![]() 、
、![]() 两家超市往年同期各50天的该食品销售记录,得到如下数据:
两家超市往年同期各50天的该食品销售记录,得到如下数据:
销售件数 | 8 | 9 | 10 | 11 |
频数 | 20 | 40 | 20 | 20 |
以这些数据的频数代替两家超市的食品销售件数的概率,记![]() 表示这两家超市每日共销售食品件数,
表示这两家超市每日共销售食品件数,![]() 表示销售公司每日共需购进食品的件数.
表示销售公司每日共需购进食品的件数.
(1)求![]() 的分布列;
的分布列;
(2)以销售食品利润的期望为决策依据,在![]() 与
与![]() 之中选其一,应选哪个?
之中选其一,应选哪个?
【答案】(1)见解析;(2) ![]() .
.
【解析】
(1)由已知一家超市销售食品件数8,9,10,11,得![]() 取值为16,17,18,19,20,21,求出相应的概率即可;
取值为16,17,18,19,20,21,求出相应的概率即可;
(2)分别列出n=19,n=20的分布列,求出相应的期望,比较即可.
(1)由已知一家超市销售食品件数8,9,10,11的概率分别为![]() .
.
![]() 取值为16,17,18,19,20,21.
取值为16,17,18,19,20,21.
![]() ,
,![]() ;
;
![]() ;
; ![]() ;
;
![]() ;
; ![]()
![]()
所以![]() 的分布列为
的分布列为
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
|
|
|
|
|
|
|
|
(2) 当![]() 时,记
时,记![]() 为
为![]() 销售该食品利润,则
销售该食品利润,则![]() 的分布列为
的分布列为
| 1450 | 1600 | 1750 | 1900 | 1950 | 2000 | 2050 |
|
|
|
|
|
|
|
|
![]()
![]()
当![]() 时,记
时,记![]() 为
为![]() 销售该食品利润,则
销售该食品利润,则![]() 的分布列为
的分布列为
| 1400 | 1550 | 1700 | 1850 | 2000 | 2050 | 2100 |
|
|
|
|
|
|
|
|
![]()
![]()
因为![]() ,故应选
,故应选![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 为正方形
为正方形![]() 内一点,它到边
内一点,它到边![]() ,
,![]() 的距离分别是1,2,
的距离分别是1,2,![]() 平面
平面![]() ,
,![]() ,
,![]() 是棱
是棱![]() 上一点,且
上一点,且![]() ,
,
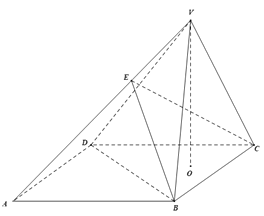
(1)求直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,我国农村7亿多贫困人口摆脱贫困,贫困发生率由1978年的97.5%下降到2018年底的1.4%,创造了人类减贫史上的中国奇迹,为全球减贫事业贡献了中国智慧和中国方案.“贫困发生率”是指低于贫困线的人口占全体人口的比例.2012年至2018年我国贫困发生率的数据如下表:
年份( | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
贫困发生率 | 10.2 | 8.5 | 7.2 | 5.7 | 4.5 | 3.1 | 1.4 |
(1)从表中所给的7个贫困发生率数据中任选两个,求至少有一个低于5%的概率;
(2)设年份代码![]() ,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
,利用回归方程,分析2012年至2018年贫困发生率的变化情况,并预测2019年贫困发生率.
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: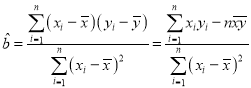 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com