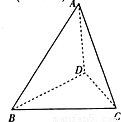
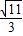分析:(1)确定∠A1CA为A1C与平面ABCD所成角,即可求直线A1C与平面ABCD所成角的正弦的值;
(2)根据线面平行的判定定理可得:D1B1∥平面GEF,同理AB1∥平面GEF,进而根据面面平行的判定定理可得面面平行;
(3)先证明EF⊥平面AA1C,再根据面面垂直的判定定理可得面面垂直.
解答:解:(1)∵A
1C∩平面ABCD=C,在正方体ABCD-A
1B
1C
1D
1,A
1A⊥平面ABCD
∴AC为A
1C在平面ABCD的射影
∴∠A
1CA为A
1C与平面ABCD所成角
∵正方体的棱长为a
∴AC=
a,A
1C=
a
∴sin∠A
1CA=
=
;
(2)在正方体ABCD-A
1B
1C
1D
1中连接BD,

因为DD
1∥B
1B,DD
1=B
1B,DD
1BB
1为平行四边形
所以D
1B
1∥DB.
∵E,F分别为BC,CD的中点
∴EF∥BD,
∴EF∥D
1B
1.
∵EF?平面GEF,D
1B
1?平面GEF,
∴D
1B
1∥平面GEF
同理AB
1∥平面GEF
∵D
1B
1∩AB
1=B
1∴平面A B
1D
1∥平面EFG.
(3)在正方体ABCD-A
1B
1C
1D
1中有AA
1⊥平面ABCD,
∵EF?平面ABCD∴AA
1⊥EF
∵ABCD为正方形
∴AC⊥BD
∵EF∥BD∴AC⊥EF.
又因为AA
1∩AC=A,
所以EF⊥平面AA
1C.
∵EF?平面EFG
∴平面AA
1C⊥面EFG.
点评:解决此类问题的关键是熟练掌握几何体的结构特征,进而利用有关的定理解决点、线、面之间的位置关系.

 如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.
如图,在棱长为ɑ的正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点.