
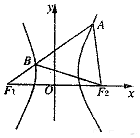
 如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1,F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦点,过F1的直线l与双曲线分别交于点A,B,且A(1,$\sqrt{3}$),若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据双曲线的定义算出△AF1F2中,|AF1|=2a,|AF2|=4a,由△ABF2是等边三角形得∠F1AF2=120°,利用余弦定理算出c2=7a2,结合A(1,$\sqrt{3}$)在双曲线上,即可得出结论.
解答 解:根据双曲线的定义,可得|AF1|-|AF2|=2a,
∵△ABF2是等边三角形,即|AF2|=|AB|
∴|BF1|=2a
又∵|BF2|-|BF1|=2a,
∴|BF2|=|BF1|+2a=4a,
∵△BF1F2中,|BF1|=2a,|BF2|=4a,∠F1BF2=120°
∴|F1F2|2=|BF1|2+|BF2|2-2|BF1|•|BF2|cos120°
即4c2=4a2+16a2-2×2a×4a×(-$\frac{1}{2}$)=28a2,
解得c2=7a2,
∴b2=c2-a2=6a2,所以双曲线方程为$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{6{a}^{2}}$=1,
又A(1,$\sqrt{3}$),在双曲线上,所以$\frac{1}{{a}^{2}}-\frac{3}{6{a}^{2}}$=1,解得a=$\frac{\sqrt{2}}{2}$.
所以△BF1F2的面积为$\frac{1}{2}×2a×4a×sin120°$=$2\sqrt{3}{a}^{2}$=$\sqrt{3}$,
故选C.
点评 本题主要考查双曲线的定义和简单几何性质等知识,根据条件求出a,b的关系是解决本题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
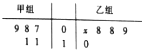 如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.
如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,0)与(0,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com