
【题目】已知数列![]() 是等差数列,数列
是等差数列,数列![]() 是等比数列,且
是等比数列,且![]() ,
,![]() 的前n项和为
的前n项和为![]() .若
.若![]() 对任意的
对任意的![]() 恒成立.
恒成立.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足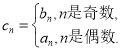 问:是否存在正整数
问:是否存在正整数![]() ,使得
,使得![]() ,若存在求出
,若存在求出![]() 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(3)若存在各项均为正整数公差为![]() 的无穷等差数列
的无穷等差数列![]() ,满足
,满足![]() ,且存在正整数
,且存在正整数![]() ,使得
,使得![]() 成等比数列,求
成等比数列,求![]() 的所有可能的值.
的所有可能的值.
【答案】(1)![]() ,
,![]() .(2)存在,
.(2)存在,![]() 的值为5和
的值为5和![]() .(3)
.(3)![]() 或
或![]() .
.
【解析】
(1)由题意可知![]() ,从而有
,从而有![]() ,做差得到
,做差得到![]() ,代入基本量计算可求出数列
,代入基本量计算可求出数列![]() ,
,![]() 的通项公式. (2)讨论
的通项公式. (2)讨论![]() 为奇数和偶数两种情况,分别代入求解计算. (3)设
为奇数和偶数两种情况,分别代入求解计算. (3)设![]() 的公差为
的公差为![]() ,则
,则![]() 且
且![]() ,若
,若![]() ,则
,则![]() 肯定成立,只需讨论
肯定成立,只需讨论![]() 时的情况即可.
时的情况即可.
(1)当![]() 时,
时,![]() ,由
,由![]() ,得
,得![]() ;
;
由![]() 得
得![]() ①,当
①,当![]() 时有:
时有:![]() ②,
②,
由②-①得![]() .
.
分别令![]() 可得:
可得:![]() ,
,![]() .设
.设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,
,
则 解得
解得![]() 或
或
经检验![]() 符合条件,
符合条件, 不合题意,舍去.
不合题意,舍去.
故![]() ,
,![]() .
.
(2)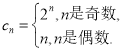
当![]() 是奇数时,由
是奇数时,由![]() ,可得
,可得![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
考虑到![]() 在正整数集上分别单调递增和递减,
在正整数集上分别单调递增和递减,
故不存在其他解,即![]() 是惟一解.
是惟一解.
当![]() 是偶数时,由
是偶数时,由![]() 可得:
可得:![]() ,
,
即![]() ,
,![]() 是偶数符合条件.
是偶数符合条件.
综上![]() 的值为5和
的值为5和![]() .
.
(3)由(1)![]() ,设
,设![]() 的公差为
的公差为![]() ,则
,则![]() 且
且![]() ,
,
当![]() 时,显然成立;
时,显然成立;
当![]() 时,
时,![]()
所以![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
即![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
所以![]()
故![]()
![]() ,
,
由![]() ,得
,得![]() ,
,
从而要使![]() ,只要
,只要![]() ,
,
又![]() ,
,
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图所示,折线图和条形图分别为某位职员2018年与2019年的家庭总收入各种用途所占比例的统计图,已知2018年的家庭总收入为10万元,2019年的储蓄总量比2018年的储蓄总量减少了10%,则下列说法:
①2019年家庭总收入比2018年增长了8%;
②年衣食住的总费用与2018年衣食住的总费相同;
③2019年的旅行总费用比2018年增加了2800元;
④2019年的就医总费用比2018年增长了5%
其中正确的个数为( )
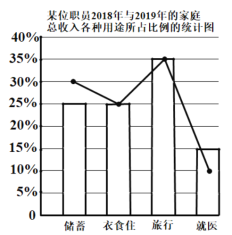
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() 为直线
为直线![]() 的倾斜角),以坐标原点
的倾斜角),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 时直线
时直线![]() 的普通方程;
的普通方程;
(2)直线![]() 和曲线
和曲线![]() 交于
交于![]() 、
、![]() 两点,点
两点,点![]() 的直角坐标为
的直角坐标为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() 是常数,且
是常数,且![]() ),曲线
),曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求![]() 的值;
的值;
(2)若存在![]() (其中
(其中![]() 是自然对数的底),使得
是自然对数的底),使得![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)设![]() ,若对任意
,若对任意![]() ,均存在
,均存在![]() ,使得方程
,使得方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
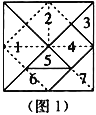
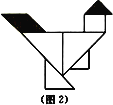
【题目】七巧板是一种古老的中国传统智力玩具,是由七块板组成.而这七块板可拼成许多图形,人物、动物、建筑物等,在18世纪,七巧板流传到了国外,至今英国剑桥大学的图书馆里还珍藏着一部《七巧图谱》.若用七巧板(图1为正方形),拼成一只雄鸡(图2),在雄鸡平面图形上随机取一点,则恰好取自雄鸡鸡头或鸡尾(阴影部分)的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加诗词大赛,各答3道题,每人答对每道题的概率均为![]() ,且各人是否答对每道题互不影响.
,且各人是否答对每道题互不影响.
(Ⅰ)用![]() 表示甲同学答对题目的个数,求随机变量
表示甲同学答对题目的个数,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅱ)设![]() 为事件“甲比乙答对题目数恰好多2”,求事件
为事件“甲比乙答对题目数恰好多2”,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com