练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数，世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段，可以用指数模型：描述累计感染病例数I(t)随时间t(单位:天)的变化规律，指数增长率r与R0，T近似满足R0 =1+rT.有学者基于已有数据估计出R0=3.28，T=6.据此，在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间约为(ln2≈0.69) （ ）

    A.1.2天B.1.8天

    C.2.5天D.3.5天

    【答案】B

    【解析】

    根据题意可得，设在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间为天，根据，解得即可得结果.

    因为，，，所以，所以，

    设在新冠肺炎疫情初始阶段，累计感染病例数增加1倍需要的时间为天，

    则，所以，所以，

    所以天.

    故选：B.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列的前n项和， 是等差数列，且.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）令.求数列的前n项和.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为（为参数）.以原点为极点，以轴为非负半轴为极轴建立极坐标系，两坐标系相同的长度单位.圆的方程为被圆截得的弦长为.

    （Ⅰ）求实数的值；

    （Ⅱ）设圆与直线交于点，若点的坐标为，且，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆，抛物线，点A是椭圆与抛物线的交点，过点A的直线l交椭圆于点B，交抛物线于M（B，M不同于A）．

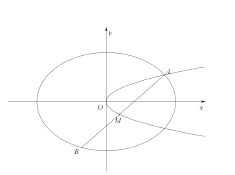
    （Ⅰ）若，求抛物线的焦点坐标；

    （Ⅱ）若存在不过原点的直线l使M为线段AB的中点，求p的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，对任意，都有.

    （1）求实数m的取值范围；

    （2）若当时，恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）当时，求曲线y=f（x）在点（1，f（1））处的切线与两坐标轴围成的三角形的面积；

    （2）若f（x）≥1，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，点P在直线上运动，请点Q满足，记点Q的为曲线C.

    （1）求曲线C的方程；

    （2）设，过点D的直线交曲线C于A，B两个不同的点，求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知抛物线E：（）与圆O：相交于A，B两点，且.过劣弧上的动点作圆O的切线交抛物线E于C，D两点，分别以C，D为切点作抛物线E的切线，，相交于点M.

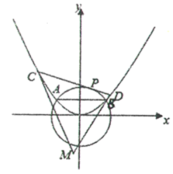
    （1）求抛物线E的方程；

    （2）求点M到直线距离的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图是某学校高三年级的三个班在一学期内的六次数学测试的平均成绩y关于测试序号x的函数图象，为了容易看出一个班级的成绩变化，将离散的点用虚线连接，根据图象，给出下列结论：

    ①一班成绩始终高于年级平均水平，整体成绩比较好；

    ②二班成绩不够稳定，波动程度较大；

    ③三班成绩虽然多次低于年级平均水平，但在稳步提升.

    其中错误的结论的个数为（ ）

    A.0B.1C.2D.3

    查看答案和解析>>

    同步练习册答案