【题目】为了了解某市开展群众体育活动的情况，拟采用分层抽样的方法从A、B、C三个区抽取5个工厂进行调查．已知这三个区分别有9，18，18个工厂．
（1）求从A、B、C三个区中分别抽取的工厂的个数；
（2）若从抽得的5个工厂中随机地抽取2个进行调查结果的比较，计算这2个工厂中至少有一个来自C区的概率．
【答案】（1）A区：1个，B区：2个，C区：2个（2）
【解析】
（1）先计算
区中工厂数的比例，再利用分层抽样方法，根据比例计算各区应抽取的工厂数；（2）利用列举法，先将各区所抽取的工厂用字母表达，分别列举出从抽取的5个工厂中随机抽取2个的事件和至少有1个来自
区的事件，再利用古典概型概率公式求解即可．
（1）工厂总数为9+18+18=45，
样本容量与总体中的个体数比为
，
所以从A，B，C三个区中应分别抽取的工厂个数为：
A区：1个B区：2个C区：2个
（2）抽得的5个工厂分别记作A，B1，B2，C1，C2
列举列举出从抽取的5个工厂中随机抽取2个的事件：（A，B1）（A1，B2）（A，C1）（A，C2）（B1，B2）（B1，C1）（B1，C2）（B2，C1）（B2，C2）（C1，C2）共10个；
至少有1个来自区的事件（A，C1）（A，C2）（B1，C1）（B1，C2）（B2，C1）（B2，C2）（C1，C2）共7个，从抽得的5个工厂中随机地抽取2个进行调查结果的比较，这2个工厂中至少有一个来自C区的概率.
提分百分百检测卷系列答案
宝贝计划期末冲刺夺100分系列答案
能考试全能100分系列答案科目：高中数学 来源： 题型：
【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点．
（1）证明MN∥平面PAB；
（2）求四面体N﹣BCM的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
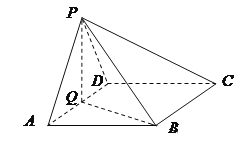
【题目】如图，四棱锥
中，底面ABCD为菱形，
，Q是AD的中点.
（Ⅰ）若
，求证：平面PQB
平面PAD；
（Ⅱ）若平面APD平面ABCD，且
，点M在线段PC上，试确定点M的位置，使二面角
的大小为
，并求出
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某同学在研究函数f（x）=
（x∈R）时，分别给出下面几个结论：
①等式f（-x）=-f（x）在x∈R时恒成立；
②函数f（x）的值域为（-1，1）；
③若x1≠x2，则一定有f（x1）≠f（x2）；
④方程f（x）=x在R上有三个根．
其中正确结论的序号有______．（请将你认为正确的结论的序号都填上）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数f（x）=x3+ax2+bx+c．
（1）求曲线y=f（x）在点（0，f（0））处的切线方程；
（2）设a=b=4，若函数f（x）有三个不同零点，求c的取值范围；
（3）求证：a2﹣3b＞0是f（x）有三个不同零点的必要而不充分条件．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列叙述：
①化简
的结果为﹣
．
②函数y＝
在（﹣∞，﹣1）和（﹣1，+∞）上是减函数；
③函数y＝log3x+x2﹣2在定义域内只有一个零点；
④定义域内任意两个变量x1，x2，都有
，则f（x）在定义域内是增函数．
其中正确的结论序号是_____
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的首项为1，Sn为数列{an}的前n项和，Sn+1=qSn+1，其中q＞0，n∈N+
（1）若a2 ， a3 ， a2+a3成等差数列，求数列{an}的通项公式；
（2）设双曲线x2﹣ 
=1的离心率为en ， 且e2=2，求e12+e22+…+en2 ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在正三棱柱ABC-A1B1C1，底面△ABC的边长AB=1，侧棱长为
，P是A1B1的中点，E、F、G分别是AC，BC，PC的中点．
（1）求FG与BB1所成角的大小；
（2）求证：平面EFG∥平面ABB1A1．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
