
【题目】在平面直角坐标系xOy中,已知点![]() ,
,![]() .
.
![]() 求
求![]() 的值;
的值;
![]() 若
若![]() 的平分线交线段AB于点D,求点D的坐标;
的平分线交线段AB于点D,求点D的坐标;
![]() 在单位圆上是否存在点C,使得
在单位圆上是否存在点C,使得![]() ?若存在,请求出点C的坐标;若不存在,请说明理由.
?若存在,请求出点C的坐标;若不存在,请说明理由.
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
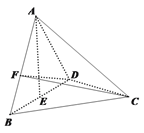
【题目】如图,在三棱锥![]() 中,已知
中,已知![]() 都是边长为
都是边长为![]() 的等边三角形,
的等边三角形,![]() 为
为![]() 中点,且
中点,且![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 上一动点,记
上一动点,记![]() .
.
(1)当![]() 时,求异面直线
时,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)当![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2+y2≤4确定的平面区域为U,|x|+|y|≤1确定的平面区域为V.
(1)定义横、纵坐标为整数的点为“整点”,在区域U内任取3个整点,求这些整点中恰有2个整点在区域V的概率;
(2)在区域U内任取3个点,记这3个点在区域V的个数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中.侧梭长均为4.底边AC=4.AB=2,BC=2 ![]() ,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
,D.E分别为PC.BC的中点. 〔I)求证:平面PAC⊥平面ABC.
(Ⅱ)求三棱锥P﹣ABC的体积;
(Ⅲ)求二面角C﹣AD﹣E的余弦值.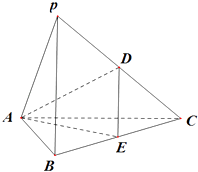
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上的![]() 件产品作为样本,称出它们的重量(单位:克),重量的分组区间为
件产品作为样本,称出它们的重量(单位:克),重量的分组区间为![]() ,
,![]() ,…,
,…,![]() ,由此得到样本的频率分布方图,如图所示.
,由此得到样本的频率分布方图,如图所示.
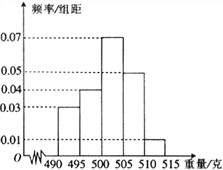
(1)在上述抽取的![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的概率;
的概率;
(2)从上述![]() 件产品中任取
件产品中任取![]() 件,设
件,设![]() 为取到重量超过
为取到重量超过![]() 克的产品件数,求
克的产品件数,求![]() 的分布列与期望.
的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“傻子瓜子”是著名瓜子品牌,芜湖特产之一.屯溪一中组织高二年级赴芜湖方特进 行研学活动,开拓视野,甲、乙两名同学在活动结束之余准备赴商场购买一定量的傻子瓜子.为了让本次研学活动具有实际意义,两名同学经过了解得知![]() 系列的瓜子不仅便宜而且口味还不错,并且每日的销售量
系列的瓜子不仅便宜而且口味还不错,并且每日的销售量![]() (单位:千克)与销售价格
(单位:千克)与销售价格![]() (元/千克)满足关系式:
(元/千克)满足关系式:![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为5元/千克时,每日可售出
为常数.已知销售价格为5元/千克时,每日可售出![]() 系列瓜子11千克.若
系列瓜子11千克.若![]() 系列瓜子的成本为3元/千克,试确定销售价格
系列瓜子的成本为3元/千克,试确定销售价格![]() 的值,使该商场每日销售
的值,使该商场每日销售![]() 系列瓜子所获得的利润最大.
系列瓜子所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某镇在政府“精准扶贫”的政策指引下,充分利用自身资源,大力发展养殖业,以增加收入,政府计划共投入72万元,全部用于甲、乙两个合作社,每个合作社至少要投入15万元,其中甲合作社养鱼,乙合作社养鸡,在对市场进行调研分析发现养鱼的收益![]() 、养鸡的收益
、养鸡的收益![]() 与投入
与投入![]() (单位:万元)满足
(单位:万元)满足![]()
![]() .设甲合作社的投入为
.设甲合作社的投入为![]() (单位:万元).两个合作社的总收益为
(单位:万元).两个合作社的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲合作社的投入为25万元时,求两个合作社的总收益;
(2)试问如何安排甲、乙两个合作的投入,才能使总收益最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点![]() ,且与圆M:
,且与圆M:![]() 关于直线
关于直线![]() 对称.
对称.
![]() 求圆C的方程;
求圆C的方程;
![]() 过点P作两条相异直线分别与圆C相交于点A和点B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
过点P作两条相异直线分别与圆C相交于点A和点B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com