
【题目】某厂生产不同规格的一种产品,根据检测标准,其合格产品的质量![]() 与尺寸x(mm)之间近似满足关系式
与尺寸x(mm)之间近似满足关系式![]() (b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间
(b、c为大于0的常数).按照某项指标测定,当产品质量与尺寸的比在区间![]() 内时为优等品.现随机抽取6件合格产品,测得数据如下:
内时为优等品.现随机抽取6件合格产品,测得数据如下:
尺寸x(mm) | 38 | 48 | 58 | 68 | 78 | 88 |
质量y (g) | 16.8 | 18.8 | 20.7 | 22.4 | 24 | 25.5 |
质量与尺寸的比 | 0.442 | 0.392 | 0.357 | 0.329 | 0.308 | 0.290 |
(Ⅰ)现从抽取的6件合格产品中再任选3件,记![]() 为取到优等品的件数,试求随机变量
为取到优等品的件数,试求随机变量![]() 的分布列和期望;
的分布列和期望;
(Ⅱ)根据测得数据作了初步处理,得相关统计量的值如下表:
|
|
|
|
75.3 | 24.6 | 18.3 | 101.4 |
(ⅰ)根据所给统计量,求y关于x的回归方程;
(ⅱ)已知优等品的收益![]() (单位:千元)与
(单位:千元)与![]() 的关系为
的关系为![]() ,则当优等品的尺寸x为何值时,收益
,则当优等品的尺寸x为何值时,收益![]() 的预报值最大?(精确到0.1)
的预报值最大?(精确到0.1)
附:对于样本![]()
![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: ,
,![]() ,
,![]() .
.
【答案】(1)见解析(2)![]() ,x=72.3
,x=72.3
【解析】
![]() 由题意,首先确定
由题意,首先确定![]() 的取值,然后求解相应的分布列和数学期望即可
的取值,然后求解相应的分布列和数学期望即可
![]()
![]() 结合题中所给的数据计算回归方程即可
结合题中所给的数据计算回归方程即可
![]() 结合计算求得的回归方程得到收益函数,讨论函数的最值即可求得最终结果
结合计算求得的回归方程得到收益函数,讨论函数的最值即可求得最终结果
(1)解:由已知,优等品的质量与尺寸的比在区间![]() 内,即
内,即![]()
则随机抽取的6件合格产品中,有3件为优等品,3件为非优等品
现从抽取的6件合格产品中再任选3件,则取到优等品的件数![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() 的分布列为
的分布列为
|
|
|
|
|
|
|
|
|
![]()
(2)解:对![]() (
(![]() )两边取自然对数得
)两边取自然对数得![]() ,
,
令![]() ,得
,得![]() ,且
,且![]() ,
,
(ⅰ)根据所给统计量及最小二乘估计公式有,
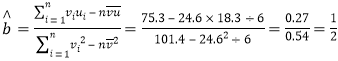 -
-
![]() ,得
,得![]() ,故
,故![]()
所求y关于x的回归方程为![]()
(ⅱ)由(ⅰ)可知,![]() ,则
,则![]()
由优等品质量与尺寸的比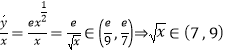 ,即
,即![]() 令
令![]() ,
,![]()
当![]() 时,
时,![]() 取最大值 -
取最大值 -
即优等品的尺寸![]() (mm),收益
(mm),收益![]() 的预报值最大.
的预报值最大.


科目:高中数学 来源: 题型:
【题目】下列说法错误的是
A. 相关关系是一种非确定性关系
B. 线性回归方程对应的直线![]() ,至少经过其样本数据点
,至少经过其样本数据点![]() 中的一个点
中的一个点
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高
D. 在回归分析中,![]() 为
为![]() 的模型比
的模型比![]() 为
为![]() 的模型拟合的效果好
的模型拟合的效果好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,人们对食品安全越来越重视,有机蔬菜的需求也越来越大,国家也制定出台了一系列支持有机肥产业发展的优惠政策,鼓励和引导农民增施有机肥,“藏粮于地,藏粮于技”.根据某种植基地对某种有机蔬菜产量与有机肥用量的统计,每个有机蔬菜大棚产量的增加量![]() (百斤)与使用有机肥料
(百斤)与使用有机肥料![]() (千克)之间对应数据如下表:
(千克)之间对应数据如下表:
使用有机肥料 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
产量增加量 | 2.1 | 2.9 | 3.5 | 4.2 | 4.8 | 5.6 | 6.2 | 6.7 |
(1)根据表中的数据,试建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (精确到
(精确到![]() );
);
(2) 若种植基地每天早上7点将采摘的某有机蔬菜以每千克10元的价格销售到某超市,超市以每千克15元的价格卖给顾客.已知该超市每天8点开始营业,22点结束营业,超市规定:如果当天16点前该有机蔬菜没卖完,则以每千克5元的促销价格卖给顾客(根据经验,当天都能全部卖完).该超市统计了100天该有机蔬菜在每天的16点前的销售量(单位:千克),如表:
每天16点前的 销售量(单位:千克) | 100 | 110 | 120 | 130 | 140 | 150 | 160 |
频数 | 10 | 20 | 16 | 16 | 14 | 14 | 10 |
若以100天记录的频率作为每天16点前销售量发生的概率,以该超市当天销售该有机蔬菜利润的期望值为决策依据,说明该超市选择购进该有机蔬菜110千克还是120千克,能使获得的利润更大?
附:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为: 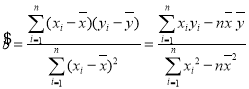 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某人做某件事,成功的概率只有0.1.用计算器计算,如果他尝试10次,而且每次是否成功都相互独立,则他至少有一次成功的概率为多少(精确到0.01)?如果他尝试20次呢?如果要保证至少成功一次的概率不小于90%,则他至少要尝试多少次?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个棱长为![]() 的正方体的表面涂上颜色,将其适当分割成棱长为
的正方体的表面涂上颜色,将其适当分割成棱长为![]() 的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()
的小正方体,全部放入不透明的口袋中,搅拌均匀后,从中任取一个,取出的小正方体表面仅有一个面涂有颜色的概率是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校在本校任选了一个班级,对全班50名学生进行了作业量的调查,根据调查结果统计后,得到如下的![]() 列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为
列联表,已知在这50人中随机抽取2人,这2人都“认为作业量大”的概率为![]() .
.
认为作业量大 | 认为作业量不大 | 合计 | |
男生 | 18 | ||
女生 | 17 | ||
合计 | 50 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否有![]() 的把握认为“认为作业量大”与“性别”有关?
的把握认为“认为作业量大”与“性别”有关?
附表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
附: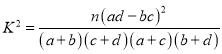 (其中
(其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为![]()
![]() 且
且![]() ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分![]() 为
为![]()
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com