
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.

(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
【答案】(1)0.32 ;(2)众数是170,中位数是168.25 ;(3)![]()
【解析】
(1)利用频率分布直方图能求出被采访人恰好在第2组或第6组的概率;
(2)利用频率分布直方图能求出众数和中位数;
(3)共50×0.12=6人,其中男生3人,设为a,b,c,女生三人,设为d,e,f,利用列举法能求出至少有1名女性市民的概率.
(1)被采访人拾好在第2组或第6组的概率![]() .
.
(2)众数:![]() ;
;
设中位数为![]() ,则
,则![]()
∴中位数![]() .
.
(3)共![]() 人,其中男生3人,设为
人,其中男生3人,设为![]() ,
,![]() ,
,![]() ,女生三人,设为
,女生三人,设为![]() ,
,![]() ,
,![]() ,则任选2人,
,则任选2人,
可能为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15种,
,共15种,
其中两个全是男生的有![]() ,
,![]() ,
,![]() ,共3种情况,
,共3种情况,
设事件![]() :至少有1名女性,则至少有1名女性市民的概率
:至少有1名女性,则至少有1名女性市民的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,现从高一学生中抽取![]() 人做调查,得到
人做调查,得到![]() 列联表:
列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 40 | ||
女生 | 30 | ||
合计 | 100 |
且已知在![]() 个人中随机抽取
个人中随机抽取![]() 人,抽到喜欢游泳的学生的概率为
人,抽到喜欢游泳的学生的概率为![]() .
.
(1)请完成上面的列联表;
(2)根据列联表的数据,是否有![]() 的把握认为喜欢游泳与性别有关?并说明你的理由.
的把握认为喜欢游泳与性别有关?并说明你的理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产某款机器零件,因为要求精度比较高,所以需要对生产的一大批零件进行质量检测.首先由专家根据各种系数制定了质量指标值,从生产的大批零件中选取100件作为样本进行评估,根据评估结果作出如图所示的频率分布直方图.
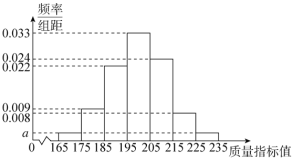
(1)(ⅰ)根据直方图求![]() 及这100个零件的样本平均数
及这100个零件的样本平均数![]() (同一组数据用该组数据区间的中点值表示);
(同一组数据用该组数据区间的中点值表示);
(ⅱ)以样本估计总体,经过专家研究,零件的质量指标值![]() ,试估计10000件零件质量指标值在
,试估计10000件零件质量指标值在![]() 内的件数;
内的件数;
(2)设每个零件利润为![]() 元,质量指标值为
元,质量指标值为![]() ,利润
,利润![]() 与质量指标值
与质量指标值![]() 之间满足函数关系
之间满足函数关系![]() .假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
.假设同组中的每个数据用该组区间的中点值代替,试估算该批零件的平均利润.(结果四舍五入,保留整数)
参考数据:![]() ,则
,则![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)记![]() 为数列
为数列![]() 的前
的前![]() 项和,是否存在正整数
项和,是否存在正整数![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S—ABCD中,![]() 底面ABCD,底面ABCD是矩形,且
底面ABCD,底面ABCD是矩形,且![]() ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED![]() 平面SAB;
平面SAB;
(2)求平面BED与平面SBC所成二面角(锐角)的大小.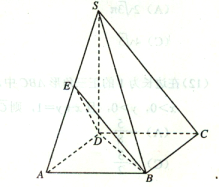
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 分别为
分别为![]() 的左顶点和上顶点,若
的左顶点和上顶点,若![]() 的中点的纵坐标为
的中点的纵坐标为![]() .
.![]() 分别为
分别为![]() 的左、右焦点.
的左、右焦点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与
与![]() 交于
交于![]() 两点,
两点,![]() ,
,![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以
在以![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com