练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在直角坐标系中，曲线的参数方程为（为参数，以坐标原点为极点，轴的正半轴为极轴，取相同长度单位建立极坐标系，曲线的极坐标方程为．

    （1）求曲线的极坐标方程和曲线的普通方程；

    （2）设射线与曲线交于不同于极点的点，与曲线交于不同于极点的点，求线段的长．

    【答案】（1）；（2）

    【解析】

    曲线的参数方程转换为直角坐标方程为．再用极直互化公式求解，曲线的极坐标方程用极直互化公式转换为直角坐标方程．

    射线与曲线的极坐标方程联解求出，射线与曲线的极坐标方程联解求出， 再用 得解

    解：曲线的参数方程为（为参数，转换为直角坐标方程为．把，代入得：

    曲线的极坐标方程为．转换为直角坐标方程为．

    设射线与曲线交于不同于极点的点，

    所以，解得．

    与曲线交于不同于极点的点，

    所以，解得，

    所以

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某小型水库的管理部门为研究库区水量的变化情况，决定安排两个小组在同一年中各自独立的进行观察研究.其中一个小组研究水源涵养情况.他们通过观察入库的若干小溪和降雨量等因素，随机记录了天的日入库水量数据（单位:千），得到下面的柱状图（如图甲）.另一小组则研究由于放水、蒸发或渗漏造成的水量消失情况.他们通过观察与水库相连的特殊小池塘的水面下降情况来研究库区水的整体消失量，随机记录了天的库区日消失水量数据（单位:千），并将观测数据整理成频率分布直方图（如图乙）.

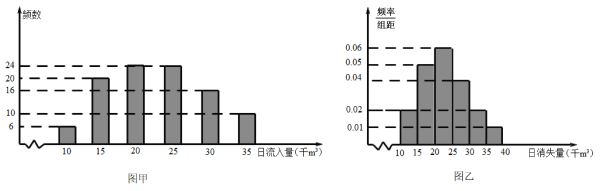
    （1）据此估计这一年中日消失水量的平均值；

    （2）以频率作为概率，试解决如下问题：

    ①分别估计日流入水量不少于千和日消失量不多于千的概率；

    ②试估计经过一年后，该水库的水量是增加了还是减少了，变化的量是多少？（一年按天计算），说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校名学生参加军事冬令营活动，活动期间各自扮演一名角色进行分组游戏，角色按级别从小到大共种，分别为士兵、排长、连长、营长、团长、旅长、师长、军长和司令.游戏分组有两种方式，可以人一组或者人一组.如果人一组，则必须角色相同；如果人一组，则人角色相同或者人为级别连续的个不同角色.已知这名学生扮演的角色有名士兵和名司令，其余角色各人，现在新加入名学生，将这名学生分成组进行游戏，则新加入的学生可以扮演的角色的种数为________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四边形ABCD为平行四边形，点E在AB上，AE＝2EB＝2，且DE⊥AB.以DE为折痕把△ADE折起，使点A到达点F的位置，且∠FEB＝60°.

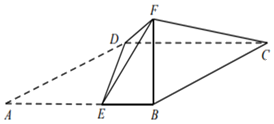
    （1）求证：平面BFC⊥平面BCDE；

    （2）若直线DF与平面BCDE所成角的正切值为，求二面角E﹣DF﹣C的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知焦点在轴上的椭圆的一个顶点为，以右焦点为圆心以3为半径的圆与直线相切．

    （1）求椭圆的方程；

    （2）设椭圆与直线相交于不同的两点、．当时，求三角形面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过椭圆上一点作两条直线，与椭圆另交于，点，设它们的斜率分别为，．

    （1）若，，求的面积；

    （2）若，，求直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极坐标系中，曲线C的极坐标方程为.以极点为原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为 (t为参数)

    (1)若，求曲线C的直角坐标方程以及直线l的极坐标方程；

    (2)设点，曲线C与直线 交于A、B两点，求的最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，直线的参数方程为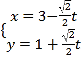（为参数），在以坐标原点为极点，轴正半轴为极轴的极坐标系中，曲线的方程为.

    （1）求曲线的直角坐标方程；

    （2）设曲线与直线交于点，点的坐标为（3，1），求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在党中央的正确指导下，通过全国人民的齐心协力，特别是全体一线医护人员的奋力救治，二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报，甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下：

    根据图中甲、乙两省的数字特征进行比对，通过比较把你得到最重要的两个结论写在答案纸指定的空白处.

    ①_________________________________________________.

    ②_________________________________________________.

    查看答案和解析>>

    同步练习册答案