
分析 分向量共线与不共线的情况,利用向量加法、减法的三角形法则做出图形,结合三角形的边的关系:“两边之和大于第三边,两边之差小于第三边”进行证明.
解答 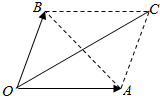 证明:分三种情况考虑.
证明:分三种情况考虑.
(1)当向量$\overrightarrow{a}$,$\overrightarrow{b}$共线且方向相同时,|$\overrightarrow{a}$|-|$\overrightarrow{b}$|<|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$|.
(2)当向量$\overrightarrow{a}$,$\overrightarrow{b}$共线且方向相反时,$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{a}$-(-$\overrightarrow{b}$),
利用(1)的结论有||$\overrightarrow{a}$|-|$\overrightarrow{b}$||<|$\overrightarrow{a}$+$\overrightarrow{b}$|<|$\overrightarrow{a}$|+|$\overrightarrow{b}$|.
(3)当向量$\overrightarrow{a}$,$\overrightarrow{b}$不共线时,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,作$\overrightarrow{OC}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{c}$,
$\overrightarrow{BA}$=$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{a}$-$\overrightarrow{b}$.
利用三角形两边之和大于第三边,两边之差小于第三边,得||$\overrightarrow{a}$|-|$\overrightarrow{b}$||≤|$\overrightarrow{a}+\overrightarrow{b}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|.
综上,结论得证.
点评 本题主要考查了平面向量的共线与不共线时两向量和(或差)的模与向量模的和(或差)的大小关系,解决问题的关键是要熟练运用向量的加法及减法的三角形法则(平行四边形法则).分类讨论的数学思想要注意掌握.


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | 向量$\overrightarrow{AB}$与向量$\overrightarrow{BA}$的长度相等 | |
| B. | 任意一个非零向量都可以平行移动 | |
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,且$\overrightarrow{b}$≠$\overrightarrow{0}$,则$\overrightarrow{a}$≠$\overrightarrow{0}$ | |
| D. | 两个有共同起点且共线的向量,其终点不一定相同. |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
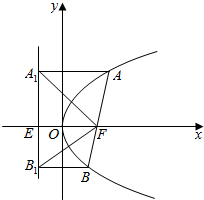 如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )
如图所示,线段AB时抛物线的焦点弦,F为抛物线焦点,若A,B在其准线上的射影分别为A1,B1,则∠A1FB1等于( )| A. | 45° | B. | 60° | C. | 90° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com